Understand the intuition behind MDPs leading to Reinforcement Learning and the Q-learning algorithm.
Reinforcement Learning¶
I would like to give full credits to the respective authors as these are my personal python notebooks taken from deep learning courses from Andrew Ng, Data School and Udemy :) This is a simple python notebook hosted generously through Github Pages that is on my main personal notes repository on https://github.com/ritchieng/ritchieng.github.io. They are meant for my personal review but I have open-source my repository of personal notes as a lot of people found it useful.
Approaches to RL
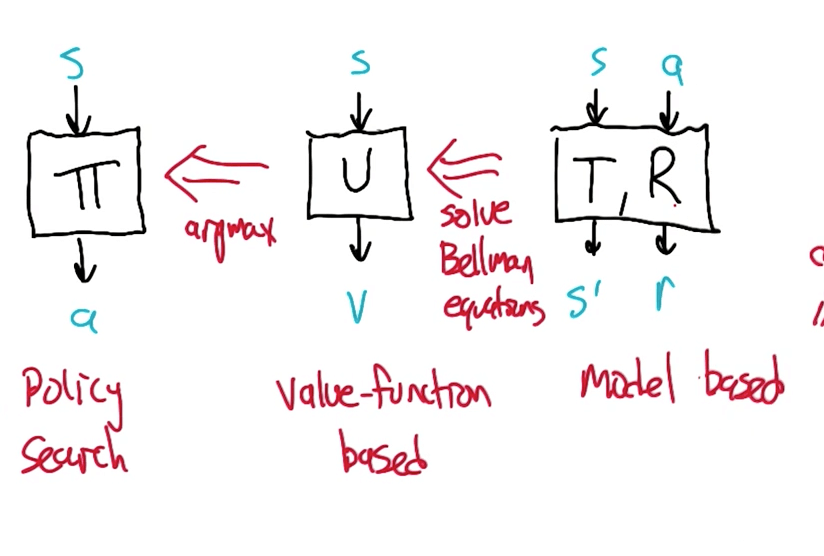
MDP's Value Function
- $$ U(s) = R(s) + γ \max_a \sum_{s'}T(s, a, s') U(s') $$
- $$ π(s) = argmax_a \sum_{s'}T(s, a, s') \ U(s') $$
Q function
- $$ Q(s, a) = R(s) + γ \sum_{s'}T(s, a, s') \max_{a'} Q(s', a') $$
- Value for arriving in s
- Leaving via a
- Proceeding optimally thereafter
Defining MDP's Value Function as Q Functions
- $$U(s) = \max_a \ Q(s, a)$$
- $$π(s) = argmax_a \ Q(s, a)$$
Q-learning
- Evaluating the Bellman equations from data.
- We need to estimate Q from transitions .
- s, a, r, s'
- We are in a state, we take an action, we get the reward and we are in the next state.
- s, a, r, s'
- We need to estimate Q from transitions .
Estimating Q from Transitions: Q-learning Equation
- $$ \hat{Q}(s, a)\leftarrow_{\alpha_t} \ r + γ \ \max_{a'} \hat{Q}(s', a') $$
- Intuition: imagine if we've an estimate of the Q function.
- We will update by taking the state and action and moving a bit.
- We have the reward and discount the maximum of the utility of the next state.
- This represents the utility function.
- $$r + γ \ \max_{a'} \hat{Q}(s', a')$$
- This represents the utility of the next state.
- $$\max_{a'} \hat{Q}(s', a')$$
- $\alpha_t$ is the learning rate.
- $ V \leftarrow_{\alpha_t} X $
- $ V \leftarrow (1-\alpha_t)V + \alpha X $
- When $\alpha = 0$, you would have no learning at all where your new value is your original value, V=V.
- When $\alpha = 1$, you would have absolute learning where you totally forget your previous value, V leaving your new value V = X.
Convergence of Q-Learning Equation
- $\hat{Q(s, a)}$ starts anywhere
- $$ \hat{Q}(s, a)\leftarrow_{\alpha_t} \ r + γ \ \max_{a'} \hat{Q}(s', a') $$
- Then $\hat{Q(s, a)} \rightarrow Q(s, a)$
- The solution to Bellman's equation
- But, this is true only if
- (s, a) is visited infinitely often.
- $\sum_t \alpha_t = ∞$ and $\sum_t \alpha^2_t < ∞$
- s' ~ T(s, a, s') and r ~ R(s)
Q-learning is a family of algorithms
- How to initialize $\hat{Q}$?
- How to decay $\alpha_t$?
- How to choose actions?
- $\epsilon$-greedy exploration
- If GLIE (Greedy Limit + Infinite Exploration) with decayed $\epsilon$
- $\hat{Q} \rightarrow Q$ and $\hat{π} \rightarrow π^*$
- $\hat{Q} \rightarrow Q$ is learning
- $\hat{π} \rightarrow π^*$ is using
- We have to note that we face an exploration-exploitation dilemma here that is a fundamental tradeoff in reinforcement learning.
- $\epsilon$-greedy exploration
Further Readings