Decision Trees, ID3, Entropy, Information again and more.
Decision Trees Classification Model¶
- Supervised Learning
- Classification
- Taking an input X
- Mapping to a discrete label y
Classification learning terms
- Instances
- Input
- Pictures
- Credit score examples
- Input
- Concept
- Function (mappings from objects to members of a set)
- Takes input and maps the input to an output
- Function (mappings from objects to members of a set)
- Target concept
- The answer we want
- The function we want
- Hypothesis Class
- Set of all concepts you're willing to entertain
- All functions we care about (classification-only)
- Sample
- Training set
- Candidate
- Concept that you think might be the target concept
- Concept = Target Concept
- Testing set
- Take candidate concept and test if it does a good job
Decision Trees Introduction
- It's simply asking a series of questions
- You'll have decision nodes
- Pick an attribute and ask a question (is sex male?)
- Values = edges (lines)
- Yes
- Ask a different question (sub-node)
- No
- Ask a different question (sub-node)
- Yes
- Values = edges (lines)
- Pick an attribute and ask a question (is sex male?)
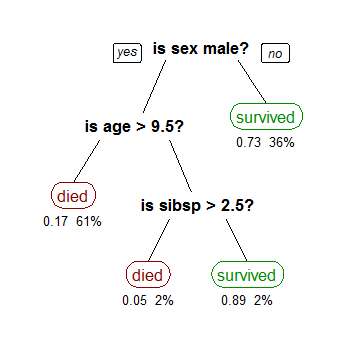
- As you can see here, you can continue to ask more questions with more nodes down the tree.
- This is an example tree from the Titanic Survivors
- As you can see here, you can continue to ask more questions with more nodes down the tree.
- Intuition
- Features' headers = questions
- sex_male
- age_>_9.5
- sibsp_>_2.5
- Features = answers
- Features' headers = questions
Decision Trees: Learning
- Pick best attribute
- Ask question
- Follow the answer path
- Go to (1)
- Repeat until you get an answer
Decision Trees: Expressiveness
- n-OR: ANY
- You need n number (linear) of nodes
- Easy!
- You need n number (linear) of nodes
- n-XOR: ODD PARITY
- If the number of attributes that are true = odd, output of the function would be true
- Otherwise, false
- You need 2^N number (exponential) of nodes
- Hard!
- If the number of attributes that are true = odd, output of the function would be true
ID3 Algorithm
- A: best attribute
- Assign A as decision attribute for node
- For each value of A, create a descendant of node
- Sort training examples to leaves
- If examples perfectly classified, stop
- Else, iterate over leaves
ID3: Bias
- Restriction Bias
- Restricted to hypothesis
- Example: only those considered in a decision tree
- Preference Bias
- What sort of hypothesis we prefer
- Inductive bias
- ID3 would prefer tree that has good splits near the top
- Prefers correct over incorrect
- Prefers shorter trees
- ID3 would prefer tree that has good splits near the top
Choosing Best Attributes: Information Gain
- Goal is to minimize entropy for maximum information gain
- Formula
- If all samples went to left side of tree
- No entropy gain in using that attribute
- Entropy constant
- If all samples went to each side of the tree with no clear split (all mixed up)
- No entropy gain
- Entropy constant
- If samples split into each side of the tree distinctly
- Max entropy gain
- Entropy fell
Decision Trees: Other Considerations
- What happens if we have continuous attributes?
- Age, weight, distance, etc.
- Create attribute with a range
- 20 <= age < 30
- This would return True or False
- You can repeat an attribute along a path for continuous attributes
- Ask 20 <= age < 30
- Ask age > 30 etc.
- But it does not make sense to repeat an attribute for discrete attributes!
- When do we stop?
- No overfitting (when the tree gets too big)!
- Solution? Pruning
- Hold out a validation set
- To build a full tree
- Cut leaves then check against validation set
- If error is low enough, stop expanding the tree
- Solution? Pruning
- No overfitting (when the tree gets too big)!
Scikit-learn for Decision Trees
In [1]:
# Import
from sklearn.tree import DecisionTreeClassifier
from sklearn.cross_validation import train_test_split
In [2]:
# Load iris dataset
from sklearn.datasets import load_iris
# Instantiate
iris = load_iris()
# Create training and feature
X = iris.data
y = iris.target
# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
In [24]:
# Same 3-step process
# 1. Instantiate
# default criterion=gini
# you can swap to criterion=entropy
dtc = DecisionTreeClassifier(random_state=0)
# 2. Fit
dtc.fit(X_train, y_train)
# 3. Predict, there're 4 features in the iris dataset
y_pred_class = dtc.predict(X_test)
Evaluating with Accuracy
In [4]:
from sklearn import metrics
In [5]:
# Accuracy
metrics.accuracy_score(y_test, y_pred_class)
Out[5]:
Dealing with overfitting: min_samples_split
- default min_samples_split=2
- This means if you've 1 sample left in a node, you cannot split further
- When it gets really deep in depth, it overfits your data
- If you increase your min_samples_split value
- You would decrease the depth of your tree
- This is because you would run out of samples to split
- This would reduce overfitting
In [11]:
# 1. Instantiate with min_samples_split = 50
dtc = DecisionTreeClassifier(min_samples_split=4, random_state=0)
# 2. Fit
dtc.fit(X_train, y_train)
# 3. Predict, there're 4 features in the iris dataset
y_pred_class = dtc.predict(X_test)
# Accuracy
metrics.accuracy_score(y_test, y_pred_class)
Out[11]:
Using GridSearchCV for optimizing parameters
In [9]:
# Import
from sklearn.grid_search import GridSearchCV
# Define the parameter values that should be searched
sample_split_range = list(range(1, 50))
# Create a parameter grid: map the parameter names to the values that should be searched
# Simply a python dictionary
# Key: parameter name
# Value: list of values that should be searched for that parameter
# Single key-value pair for param_grid
param_grid = dict(min_samples_split=sample_split_range)
# instantiate the grid
grid = GridSearchCV(dtc, param_grid, cv=10, scoring='accuracy')
# fit the grid with data
grid.fit(X_train, y_train)
Out[9]:
In [10]:
# examine the best model
# Single best score achieved across all params (min_samples_split)
print(grid.best_score_)
# Dictionary containing the parameters (min_samples_split) used to generate that score
print(grid.best_params_)
# Actual model object fit with those best parameters
# Shows default parameters that we did not specify
print(grid.best_estimator_)
Entropy
- Controls how a Decision Tree decides where to split the data
- Definition
- Measure of impurity in a bunch of examples
- Opposite of purity
- Concept
- Find variables and split
- Split such that the sets contain the least impurities
- Repeat the process until sets are pure
- Values Entropy can hold values between 0 and 1.0
- All examples same class
- Entropy = 0
- All examples are evenly split amongst classes
- Entropy = 1.0
- All examples same class
- Formula

- p(i) is the fraction of examples in class i
- sum over all classes
- Example of Formula
- Assume 2 classes for the node
- slow (2 examples)
- fast (2 examples)
- p(slow) = fraction of slow over all examples = 2/4 = 0.5
- p(fast) = fraction of fast over all examples = 2/4 = 0.5
- entropy = -p(slow)log2(pslow) + (-p(fast)log2(pslow))
- Assume 2 classes for the node
In [17]:
# Calculating impurity from the example above
# Maximum state of impurity, 1.0
import numpy as np
-0.5*np.log2(0.5) + (-0.5*np.log2(0.5))
Out[17]:
Information gain
- Formula
- information gain = entropy(parent) - [weighted average]entropy(children)
- weight = number of examples in set / total number of examples
- information gain = entropy(parent) - [weighted average]entropy(children)
- Decision tree algorithm: maximizing information gain
- Example
- Assume the feature "grade" has the following details
- Steep (Slow, S)
- Steep (Slow, S)
- Flat (Fast, F)
- Steep (Fast, F)
- If we split based on "grade": is it steep?
- Child 1: Flat (Fast)
- Child 2: Steep (Slow, Slow, Fast)
- Assume the feature "grade" has the following details
In [19]:
# Entropy of child 1 = 0
# Perfect split for this child
# Entropy of child 2 = 0.918
-(2/3)*np.log2(2/3) - (1/3)*np.log2(1/3)
Out[19]:
In [22]:
# Weighted average of entropy(children)
(3/4)*(0.9184) + (1/4)*0
Out[22]:
In [23]:
# Entropy Gain
1 - (3/4)*(0.9184) + (1/4)*0
Out[23]:
Decision Trees
- Prone to overfitting
- If you have a lot of features
- Stop growth of tree at the appropriate time
- You can build bigger classifiers out of this
- It is called ensemble classifiers
