Topics¶
- Review of model evaluation
- Model evaluation procedures
- Model evaluation metrics
- Classification accuracy
- Confusion matrix
- Metrics computed from a confusion matrix
- Adjusting the classification threshold
- Receiver Operating Characteristic (ROC) Curves
- Area Under the Curve (AUC)
- Confusion Matrix Resources
- ROC and AUC Resources
- Other Resources
This tutorial is derived from Data School's Machine Learning with scikit-learn tutorial. I added my own notes so anyone, including myself, can refer to this tutorial without watching the videos.
1. Review of model evaluation¶
- Need a way to choose between models: different model types, tuning parameters, and features
- Use a model evaluation procedure to estimate how well a model will generalize to out-of-sample data
- Requires a model evaluation metric to quantify the model performance
2. Model evaluation procedures¶
Training and testing on the same data
- Rewards overly complex models that "overfit" the training data and won't necessarily generalize
Train/test split
- Split the dataset into two pieces, so that the model can be trained and tested on different data
- Better estimate of out-of-sample performance, but still a "high variance" estimate
- Useful due to its speed, simplicity, and flexibility
- K-fold cross-validation
- Systematically create "K" train/test splits and average the results together
- Even better estimate of out-of-sample performance
- Runs "K" times slower than train/test split
3. Model evaluation metrics¶
- Regression problems: Mean Absolute Error, Mean Squared Error, Root Mean Squared Error
- Classification problems: Classification accuracy
- There are many more metrics, and we will discuss them today
4. Classification accuracy¶
Pima Indian Diabetes dataset from the UCI Machine Learning Repository
# read the data into a Pandas DataFrame
import pandas as pd
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/pima-indians-diabetes/pima-indians-diabetes.data'
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age','label']
pima = pd.read_csv(url, header=None, names=col_names)
# print the first 5 rows of data from the dataframe
pima.head()
- label
- 1: diabetes
- 0: no diabetes
- pregnant
- number of times pregnant
Question: Can we predict the diabetes status of a patient given their health measurements?
# define X and y
feature_cols = ['pregnant', 'insulin', 'bmi', 'age']
# X is a matrix, hence we use [] to access the features we want in feature_cols
X = pima[feature_cols]
# y is a vector, hence we use dot to access 'label'
y = pima.label
# split X and y into training and testing sets
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# train a logistic regression model on the training set
from sklearn.linear_model import LogisticRegression
# instantiate model
logreg = LogisticRegression()
# fit model
logreg.fit(X_train, y_train)
# make class predictions for the testing set
y_pred_class = logreg.predict(X_test)
Classification accuracy: percentage of correct predictions
# calculate accuracy
from sklearn import metrics
print(metrics.accuracy_score(y_test, y_pred_class))
Classification accuracy is 69%
Null accuracy: accuracy that could be achieved by always predicting the most frequent class
- We must always compare with this
# examine the class distribution of the testing set (using a Pandas Series method)
y_test.value_counts()
# calculate the percentage of ones
# because y_test only contains ones and zeros, we can simply calculate the mean = percentage of ones
y_test.mean()
32% of the
# calculate the percentage of zeros
1 - y_test.mean()
# calculate null accuracy in a single line of code
# only for binary classification problems coded as 0/1
max(y_test.mean(), 1 - y_test.mean())
This means that a dumb model that always predicts 0 would be right 68% of the time
- This shows how classification accuracy is not that good as it's close to a dumb model
- It's a good way to know the minimum we should achieve with our models
# calculate null accuracy (for multi-class classification problems)
y_test.value_counts().head(1) / len(y_test)
Comparing the true and predicted response values
# print the first 25 true and predicted responses
print('True:', y_test.values[0:25])
print('False:', y_pred_class[0:25])
Conclusion:
- Classification accuracy is the easiest classification metric to understand
- But, it does not tell you the underlying distribution of response values
- We examine by calculating the null accuracy
- And, it does not tell you what "types" of errors your classifier is making
5. Confusion matrix¶
Table that describes the performance of a classification model
# IMPORTANT: first argument is true values, second argument is predicted values
# this produces a 2x2 numpy array (matrix)
print(metrics.confusion_matrix(y_test, y_pred_class))
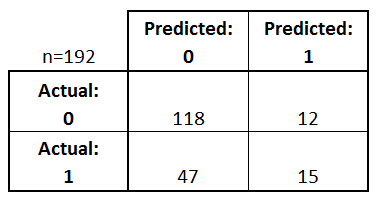
- Every observation in the testing set is represented in exactly one box
- It's a 2x2 matrix because there are 2 response classes
- The format shown here is not universal
- Take attention to the format when interpreting a confusion matrix
Basic terminology
- True Positives (TP): we correctly predicted that they do have diabetes
- 15
- True Negatives (TN): we correctly predicted that they don't have diabetes
- 118
- False Positives (FP): we incorrectly predicted that they do have diabetes (a "Type I error")
- 12
- Falsely predict positive
- Type I error
- False Negatives (FN): we incorrectly predicted that they don't have diabetes (a "Type II error")
- 47
- Falsely predict negative
- Type II error
- 0: negative class
- 1: positive class
# print the first 25 true and predicted responses
print('True', y_test.values[0:25])
print('Pred', y_pred_class[0:25])
# save confusion matrix and slice into four pieces
confusion = metrics.confusion_matrix(y_test, y_pred_class)
print(confusion)
#[row, column]
TP = confusion[1, 1]
TN = confusion[0, 0]
FP = confusion[0, 1]
FN = confusion[1, 0]
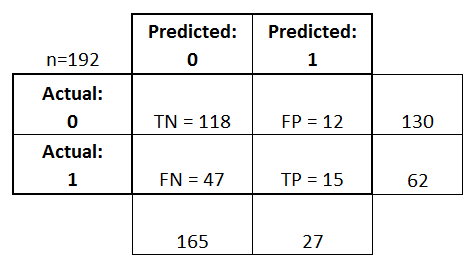
6. Metrics computed from a confusion matrix¶
Classification Accuracy: Overall, how often is the classifier correct?
# use float to perform true division, not integer division
print((TP + TN) / float(TP + TN + FP + FN))
print(metrics.accuracy_score(y_test, y_pred_class))
Classification Error: Overall, how often is the classifier incorrect?
- Also known as "Misclassification Rate"
classification_error = (FP + FN) / float(TP + TN + FP + FN)
print(classification_error)
print(1 - metrics.accuracy_score(y_test, y_pred_class))
Sensitivity: When the actual value is positive, how often is the prediction correct?
- Something we want to maximize
- How "sensitive" is the classifier to detecting positive instances?
- Also known as "True Positive Rate" or "Recall"
- TP / all positive
- all positive = TP + FN
sensitivity = TP / float(FN + TP)
print(sensitivity)
print(metrics.recall_score(y_test, y_pred_class))
Specificity: When the actual value is negative, how often is the prediction correct?
- Something we want to maximize
- How "specific" (or "selective") is the classifier in predicting positive instances?
- TN / all negative
- all negative = TN + FP
specificity = TN / (TN + FP)
print(specificity)
Our classifier
- Highly specific
- Not sensitive
False Positive Rate: When the actual value is negative, how often is the prediction incorrect?
false_positive_rate = FP / float(TN + FP)
print(false_positive_rate)
print(1 - specificity)
Precision: When a positive value is predicted, how often is the prediction correct?
- How "precise" is the classifier when predicting positive instances?
precision = TP / float(TP + FP)
print(precision)
print(metrics.precision_score(y_test, y_pred_class))
Many other metrics can be computed: F1 score, Matthews correlation coefficient, etc.
Conclusion:
- Confusion matrix gives you a more complete picture of how your classifier is performing
- Also allows you to compute various classification metrics, and these metrics can guide your model selection
Which metrics should you focus on?
- Choice of metric depends on your business objective
- Identify if FP or FN is more important to reduce
- Choose metric with relevant variable (FP or FN in the equation)
- Spam filter (positive class is "spam"):
- Optimize for precision or specificity
- precision
- false positive as variable
- specificity
- false positive as variable
- precision
- Because false negatives (spam goes to the inbox) are more acceptable than false positives (non-spam is caught by the spam filter)
- Optimize for precision or specificity
- Fraudulent transaction detector (positive class is "fraud"):
- Optimize for sensitivity
- FN as a variable
- Because false positives (normal transactions that are flagged as possible fraud) are more acceptable than false negatives (fraudulent transactions that are not detected)
- Optimize for sensitivity
7. Adjusting the classification threshold¶
# print the first 10 predicted responses
# 1D array (vector) of binary values (0, 1)
logreg.predict(X_test)[0:10]
# print the first 10 predicted probabilities of class membership
logreg.predict_proba(X_test)[0:10]
- Row: observation
- Each row, numbers sum to 1
- Column: class
- 2 response classes there 2 columns
- column 0: predicted probability that each observation is a member of class 0
- column 1: predicted probability that each observation is a member of class 1
- 2 response classes there 2 columns
- Importance of predicted probabilities
- We can rank observations by probability of diabetes
- Prioritize contacting those with a higher probability
- We can rank observations by probability of diabetes
- predict_proba process
- Predicts the probabilities
- Choose the class with the highest probability
- There is a 0.5 classification threshold
- Class 1 is predicted if probability > 0.5
- Class 0 is predicted if probability < 0.5
# print the first 10 predicted probabilities for class 1
logreg.predict_proba(X_test)[0:10, 1]
# store the predicted probabilities for class 1
y_pred_prob = logreg.predict_proba(X_test)[:, 1]
# allow plots to appear in the notebook
%matplotlib inline
import matplotlib.pyplot as plt
# adjust the font size
plt.rcParams['font.size'] = 12
# histogram of predicted probabilities
# 8 bins
plt.hist(y_pred_prob, bins=8)
# x-axis limit from 0 to 1
plt.xlim(0,1)
plt.title('Histogram of predicted probabilities')
plt.xlabel('Predicted probability of diabetes')
plt.ylabel('Frequency')
- We can see from the third bar
- About 45% of observations have probability from 0.2 to 0.3
- Small number of observations with probability > 0.5
- This is below the threshold of 0.5
- Most would be predicted "no diabetes" in this case
- Solution
- Decrease the threshold for predicting diabetes
- Increase the sensitivity of the classifier
- This would increase the number of TP
- More sensitive to positive instances
- Example of metal detector
- Threshold set to set off alarm for large object but not tiny objects
- YES: metal, NO: no metal
- We lower the threshold amount of metal to set it off
- It is now more sensitive to metal
- It will then predict YES more often
- This would increase the number of TP
- Increase the sensitivity of the classifier
- Decrease the threshold for predicting diabetes
# predict diabetes if the predicted probability is greater than 0.3
from sklearn.preprocessing import binarize
# it will return 1 for all values above 0.3 and 0 otherwise
# results are 2D so we slice out the first column
y_pred_class = binarize(y_pred_prob, 0.3)[0]
# print the first 10 predicted probabilities
y_pred_prob[0:10]
# print the first 10 predicted classes with the lower threshold
y_pred_class[0:10]
# previous confusion matrix (default threshold of 0.5)
print(confusion)
# new confusion matrix (threshold of 0.3)
print(metrics.confusion_matrix(y_test, y_pred_class))
- The row totals are the same
- The rows represent actual response values
- 130 values top row
- 62 values bottom row
- Observations from the left column moving to the right column because we will have more TP and FP
# sensitivity has increased (used to be 0.24)
print (46 / float(46 + 16))
# specificity has decreased (used to be 0.91)
print(80 / float(80 + 50))
Conclusion:
- Threshold of 0.5 is used by default (for binary problems) to convert predicted probabilities into class predictions
- Threshold can be adjusted to increase sensitivity or specificity
- Sensitivity and specificity have an inverse relationship
- Increasing one would always decrease the other
- Adjusting the threshold should be one of the last step you do in the model-building process
- The most important steps are
- Building the models
- Selecting the best model
- The most important steps are
8. Receiver Operating Characteristic (ROC) Curves¶
Question: Wouldn't it be nice if we could see how sensitivity and specificity are affected by various thresholds, without actually changing the threshold?
Answer: Plot the ROC curve.
- Receiver Operating Characteristic (ROC)
# IMPORTANT: first argument is true values, second argument is predicted probabilities
# we pass y_test and y_pred_prob
# we do not use y_pred_class, because it will give incorrect results without generating an error
# roc_curve returns 3 objects fpr, tpr, thresholds
# fpr: false positive rate
# tpr: true positive rate
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pred_prob)
plt.plot(fpr, tpr)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.rcParams['font.size'] = 12
plt.title('ROC curve for diabetes classifier')
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('True Positive Rate (Sensitivity)')
plt.grid(True)
- ROC curve can help you to choose a threshold that balances sensitivity and specificity in a way that makes sense for your particular context
- You can't actually see the thresholds used to generate the curve on the ROC curve itself
# define a function that accepts a threshold and prints sensitivity and specificity
def evaluate_threshold(threshold):
print('Sensitivity:', tpr[thresholds > threshold][-1])
print('Specificity:', 1 - fpr[thresholds > threshold][-1])
evaluate_threshold(0.5)
evaluate_threshold(0.3)
9. AUC¶
AUC is the percentage of the ROC plot that is underneath the curve:
# IMPORTANT: first argument is true values, second argument is predicted probabilities
print(metrics.roc_auc_score(y_test, y_pred_prob))
- AUC is useful as a single number summary of classifier performance
- Higher value = better classifier
- If you randomly chose one positive and one negative observation, AUC represents the likelihood that your classifier will assign a higher predicted probability to the positive observation
- AUC is useful even when there is high class imbalance (unlike classification accuracy)
- Fraud case
- Null accuracy almost 99%
- AUC is useful here
- Fraud case
# calculate cross-validated AUC
from sklearn.cross_validation import cross_val_score
cross_val_score(logreg, X, y, cv=10, scoring='roc_auc').mean()
Use both of these whenever possible
Confusion matrix advantages:
- Allows you to calculate a variety of metrics
- Useful for multi-class problems (more than two response classes)
ROC/AUC advantages:
- Does not require you to set a classification threshold
- Still useful when there is high class imbalance
10. Confusion Matrix Resources¶
- Blog post: Simple guide to confusion matrix terminology by me
- Videos: Intuitive sensitivity and specificity (9 minutes) and The tradeoff between sensitivity and specificity (13 minutes) by Rahul Patwari
- Notebook: How to calculate "expected value" from a confusion matrix by treating it as a cost-benefit matrix (by Ed Podojil)
- Graphic: How classification threshold affects different evaluation metrics (from a blog post about Amazon Machine Learning)
11. ROC and AUC Resources¶
- Lesson notes: ROC Curves (from the University of Georgia)
- Video: ROC Curves and Area Under the Curve (14 minutes) by me, including transcript and screenshots and a visualization
- Video: ROC Curves (12 minutes) by Rahul Patwari
- Paper: An introduction to ROC analysis by Tom Fawcett
- Usage examples: Comparing different feature sets for detecting fraudulent Skype users, and comparing different classifiers on a number of popular datasets
12. Other Resources¶
- scikit-learn documentation: Model evaluation
- Guide: Comparing model evaluation procedures and metrics by me
- Video: Counterfactual evaluation of machine learning models (45 minutes) about how Stripe evaluates its fraud detection model, including slides