Feature engineering and scaling with scikit-learn.
Feature Engineering: Scaling and Selection¶
Feature Scaling
- Formula
- $$X' = \frac {X - X_{min}}{X_{max} - X_{min}}$$
Algorithms affected by feature rescaling
- Algorithms in which two dimensions affect the outcome will be affected by rescaling
- SVM with RBF kernel
- When you maximize the distance, you've 2 or more dimensions
- Think of the x and y axis with different dimensions and you need to calculate the distance
- When you maximize the distance, you've 2 or more dimensions
- K-means clustering
- SVM with RBF kernel
Feature Scaling Manually in Python
In [21]:
### FYI, the most straightforward implementation might
### throw a divide-by-zero error, if the min and max values are the same
### but think about this for a second--that means that every
### data point has the same value for that feature!
### why would you rescale it? Or even use it at all?
def featureScaling(arr):
max_num = max(arr)
min_num = min(arr)
lst = []
for num in arr:
X_prime = (num - min_num) / (max_num - min_num)
lst.append(X_prime)
return lst
# tests of your feature scaler--line below is input data
data = [115, 140, 175]
print(featureScaling(data))
Feature Scaling in Scikit-learn
In [23]:
from sklearn.preprocessing import MinMaxScaler
import numpy as np
In [28]:
# 3 different training points for 1 feature
weights = np.array([[115], [140], [175]]).astype(float)
In [29]:
# Instantiate
scaler = MinMaxScaler()
In [33]:
# Rescale
rescaled_weights = scaler.fit_transform(weights)
rescaled_weights
Out[33]:
Feature Selection
- Why do we want to select features?
- Knowledge discovery
- Interpretability
- Insight
- Curse of dimensionality
- Knowledge discovery
Feature Selection: Algorithms
- How hard is the problem?
- Exponential
- $${n \choose m}$$
- $$2^n$$
- n choose m
- Assuming our original number of features: n
- New number of features: m
- Where m <= n
- Exponential
Filtering vs Wrapping
- Disadvantages of filtering
- No feedback
- Learning algorithm cannot inform on the impact of the changes in features
- Criteria built in search with no reference to the learner
- Ignores learning problem
- You'll look at features in isolation
- No feedback
- Advantages of filtering
- Fast
- Disadvantages of Wrapping
- Slow
- Advantages Wrapping
- Feedback
- Criteria built in the learner
- Takes into account model bias and learning
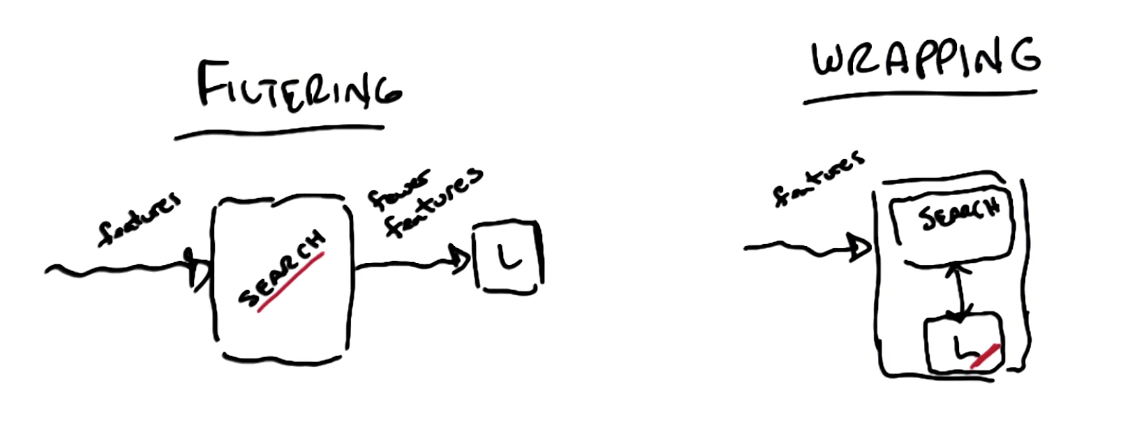
- Feedback
Filtering: Search Part
- We can use a Decision Tree algorithm for the search function then feed to the learner which does not do well with filtering features
- This is because DTs are good at filtering the best features
- If you want to know all the features, you can easily overfit
- Other generic ways
- Information gain
- Entropy
- "Useful" features
- Independent, non-redundant
Wrapping: Search Part (have to deal with the exponential problem)
- Hill climbing
- Randomized optimization
- Forward
- Start with m features
- You pass the features individually to the learning algorithms and get their scores
- You pick
- 2 features
- Choose highest score
- 3 features
- Choose highest score
- If lower than 2 features, stop
- 2 features
Relevance: Measures Effect on BOC
- X_i, feature, is strongly relevant if removing it degrades Bayes Optimal Classifier (BOC)
- BOC is the best you can do on average if you can find it
- X_i, feature, is weakly relevant if
- Not strongly relevant
- Subset of features S such that adding x_i to S improves BOC
- X_i is otherwise irrelevant
Usefulness: Measures Effect on Particular Predictor
- Minimizing error given a model/learner