K-Means algorithm, optimization objective, random initialization, and choose number of clusters.
Clustering
I would like to give full credits to the respective authors as these are my personal python notebooks taken from deep learning courses from Andrew Ng, Data School and Udemy :) This is a simple python notebook hosted generously through Github Pages that is on my main personal notes repository on https://github.com/ritchieng/ritchieng.github.io. They are meant for my personal review but I have open-source my repository of personal notes as a lot of people found it useful.
Unsupervised Learning: Introduction
- While supervised learning algorithms need labeled examples (x,y), unsupervised learning algorithms need only the input (x)
- In layman terms, unsupervised learning is learning from unlabeled data
- Supervised learning
- Given a set of labels, fit a hypothesis to it
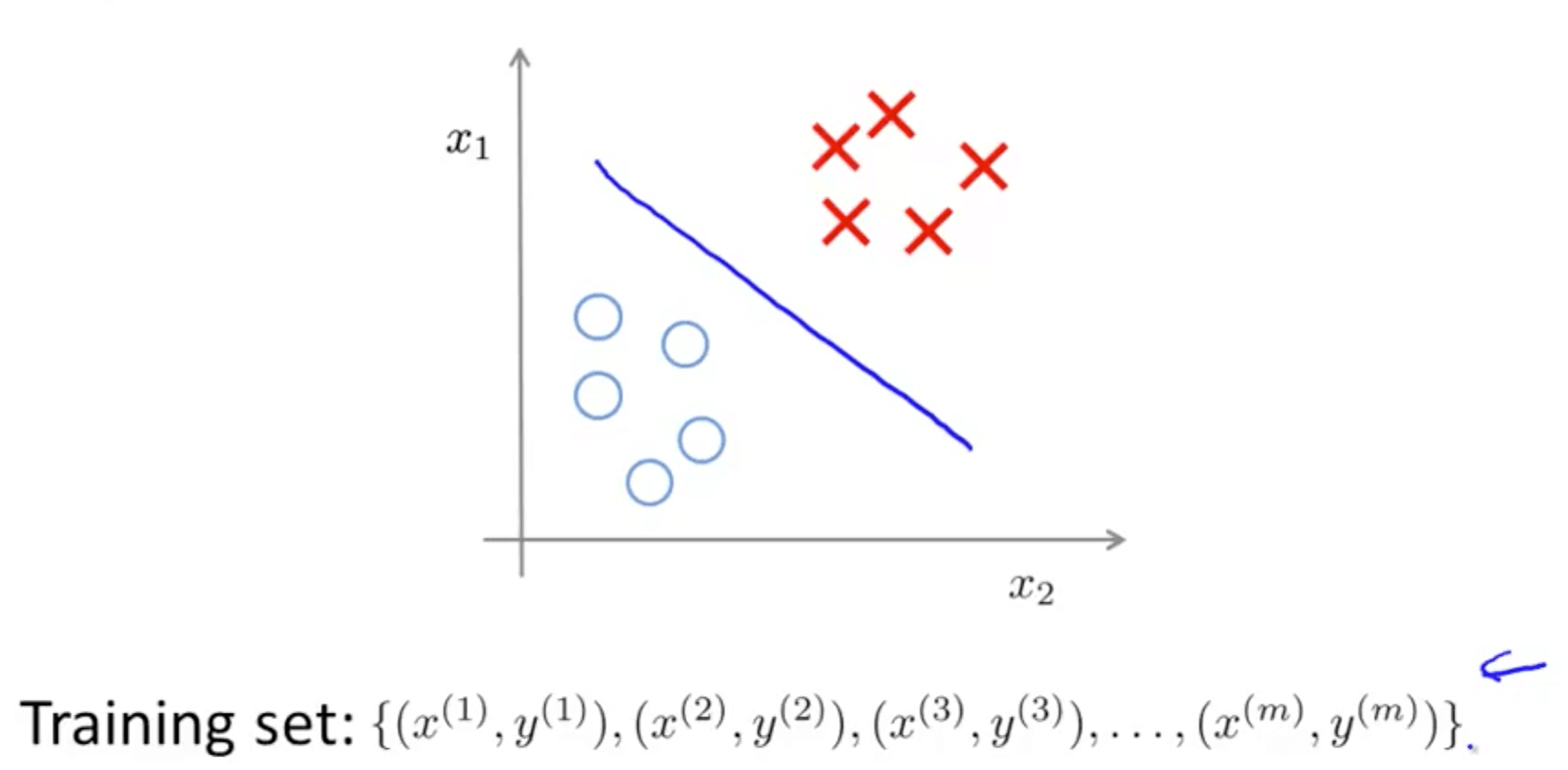
- Given a set of labels, fit a hypothesis to it
- Unsupervised learning
- No labels
- Find structure in data
- We find clusters in the data
- This is called clustering and is one of the many unsupervised learning algorithm

- This is called clustering and is one of the many unsupervised learning algorithm
- Applications of clustering
- Market segmentation
- Group people into different segments
- Social network analysis
- Smart lists
- Organize computing clusters
- Astronomical data analysis
- Understanding galaxy formation
- Market segmentation
K-Means Algorithm
- Introduction
- We want to automatically group the data into clusters
- It is the most widely used clustering algorithm
- We will choose our cluster centroids
- We have two because we want to group them into 2 clusters
- K-Means is an iterative algorithm and it does these steps
- Randomly allocate points as cluster centroids
- You can have as many, but the exact “ideal” number can be determined and will be explained subseqeuntly
- In this case, we chose 2 cluster centroids
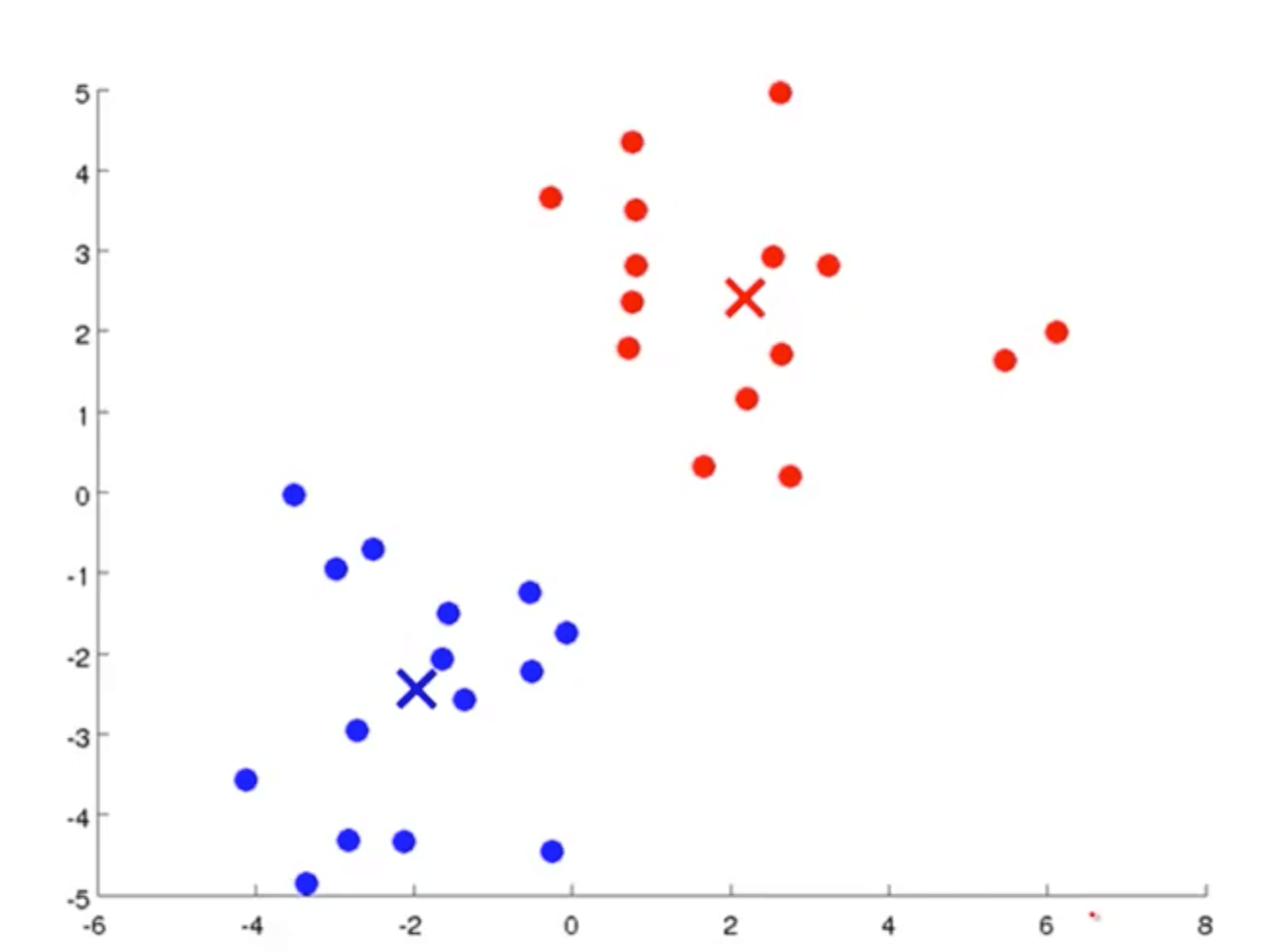
- Cluster assignment step
- What that means is that, it’s going through each of the examples, each of these green dots shown here and depending on whether it’s closer to the red cluster centroid or the blue cluster centroid, it is going to assign each of the data points to one of the two cluster centroids
- It is to go through your data set and color each of the points either red or blue, depending on whether it is closer to the red cluster centroid or the blue cluster centroid, and I’ve done that in this diagram here
- Move centroid step
- Take the two cluster centroids, that is, the red cross and the blue cross, and we are going to move them to the average of the points colored the same colour
- Look at all the red points and compute the average, the mean of the location of all the red points, and we are going to move the red cluster centroid there
- Look at all the blue dots and compute their mean, and then move the blue cluster centroid there
- Continue until it converges
- Randomly allocate points as cluster centroids
- Input

- K-means algorithm details

- K-means for non-separated clusters
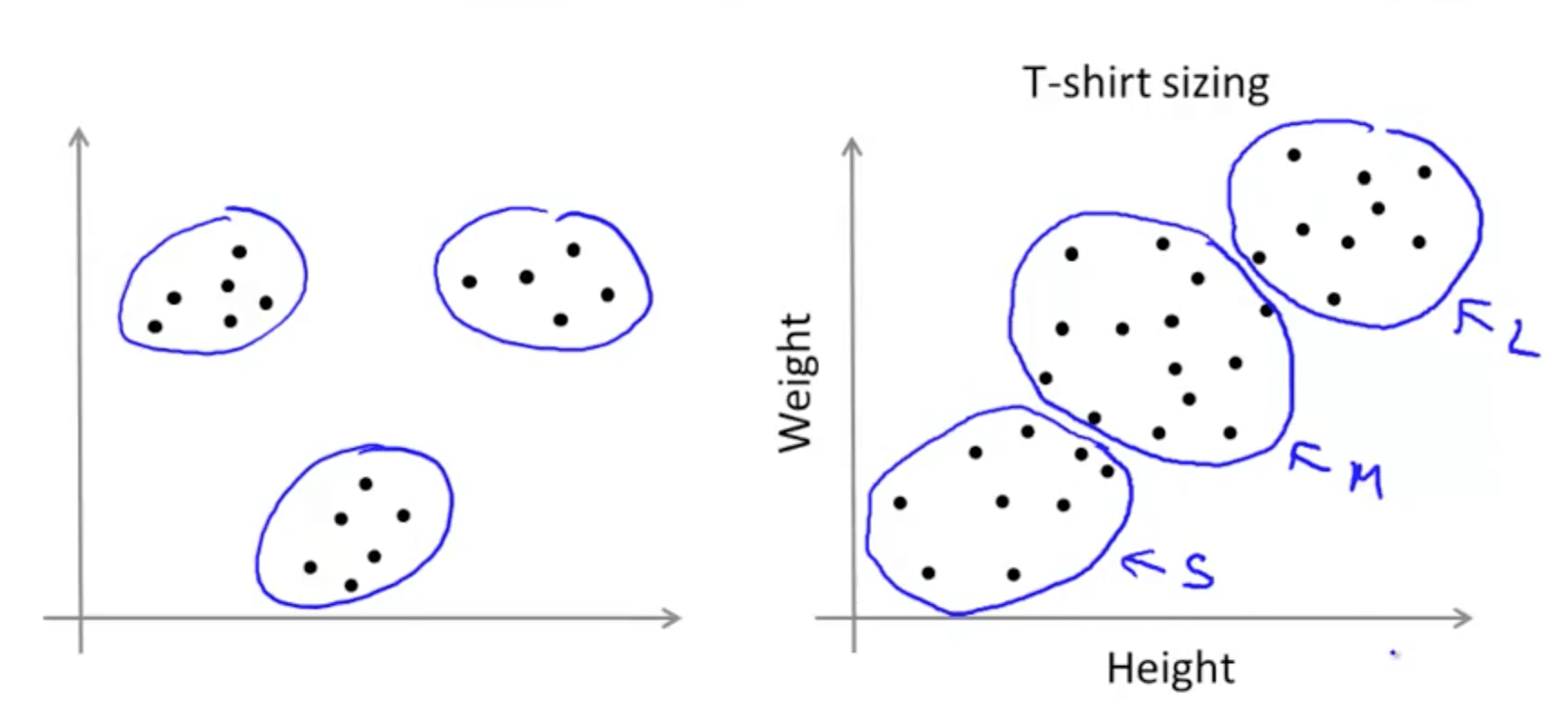
- K-means would try to separate the data into multiple clusters like the graph on the right
- Often times, you may not find clusters that are obvious like the graph on the left
- You can look at the clusters and find meaning
- For example, you can design a small, medium and large shirt based on the data shown
- It is similar to market segmentation
Optimization Objective
- K-means has a cost function to minimize (optimization objection)
- This will help us debug the algorithm
- We can use this to help K-Means find better clusters
- Cost function (distortion function)
- What it tries to do is to find c(i) and u(k) to minimize the cost function

- Steps

- Cluster assignment step keeps u(k) fixed
- Move centroid step with respect to u(k)
- What it tries to do is to find c(i) and u(k) to minimize the cost function
Random Initialization
- We need to randomly initialize K cluster centroids, but how do we do it?
- Method 1
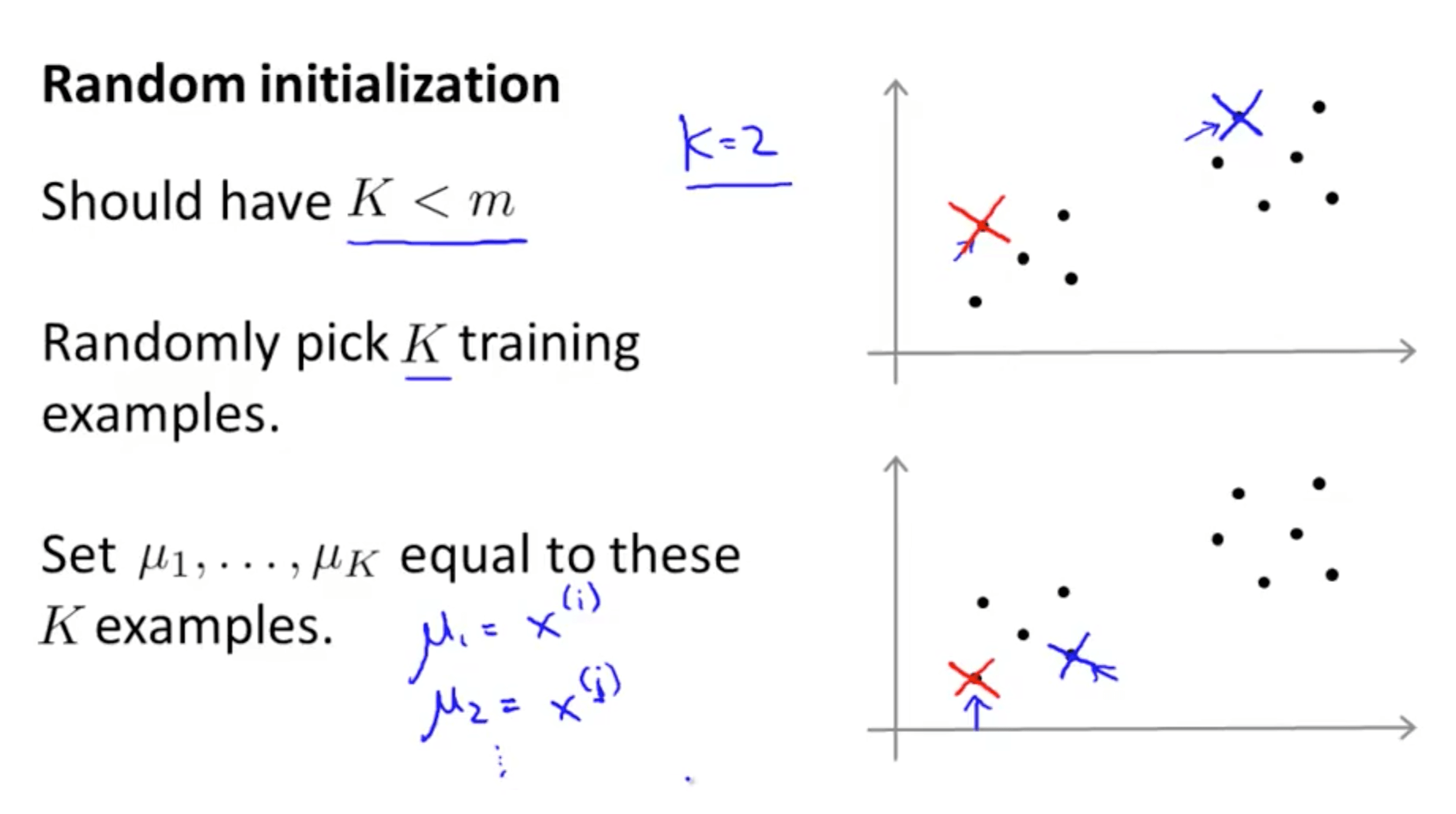
- Should have K < m
- Randomly pick K training examples - For example, picking k = 2
- Set u(1) to u(k) equal to these K examples
- Method 1
- K-means can end up at different solutions depending on different initialization
- K-means can end up in a local optima
- It might get stuck in a bad local optima
- As you can see, the bottom two graphs are not good
- The solution is to run K-means many times with different initialization
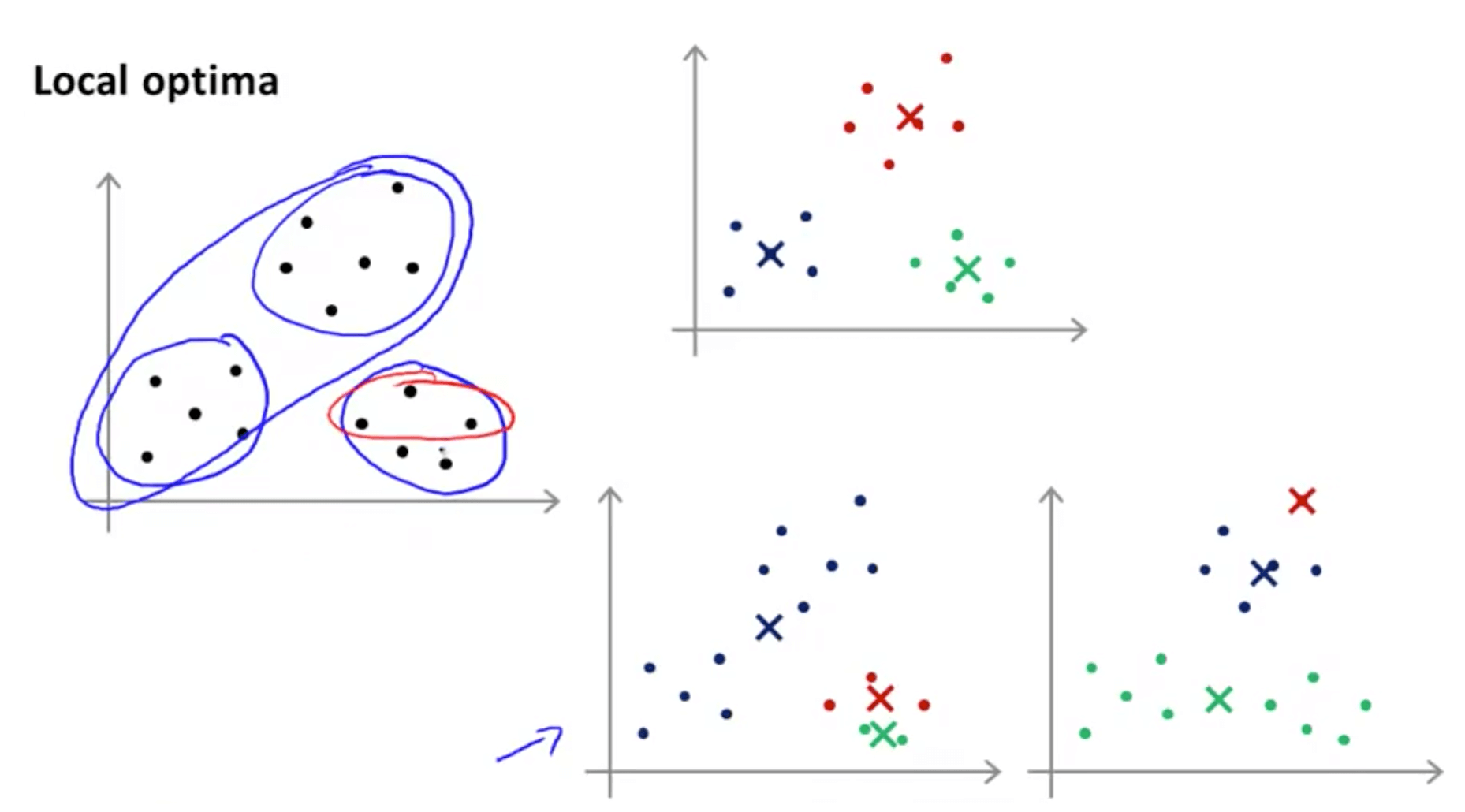
- Random Initialization Technicality

Choosing the Number of Clusters
- What is the right value of K?
- Elbow method
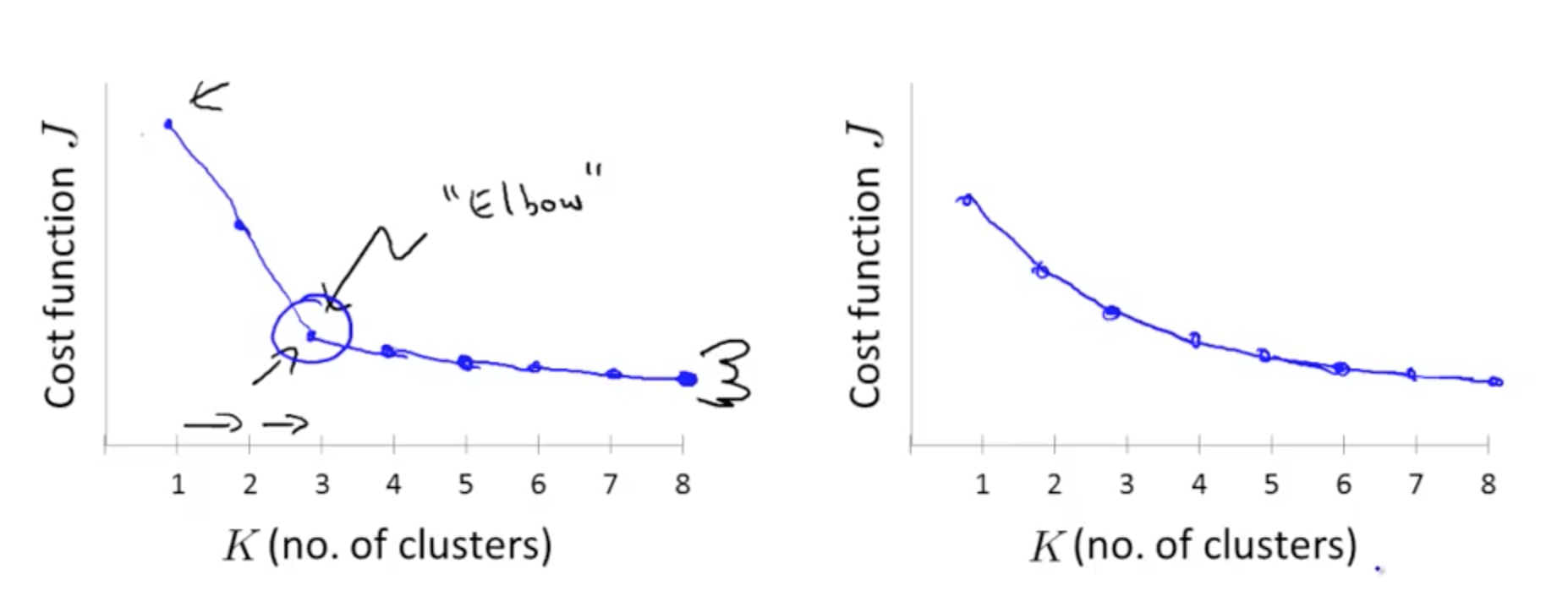
- The issue with this method is that it is not clear where the location of the elbow is
- Evaluate k-means to get clusters to use for some later purpose
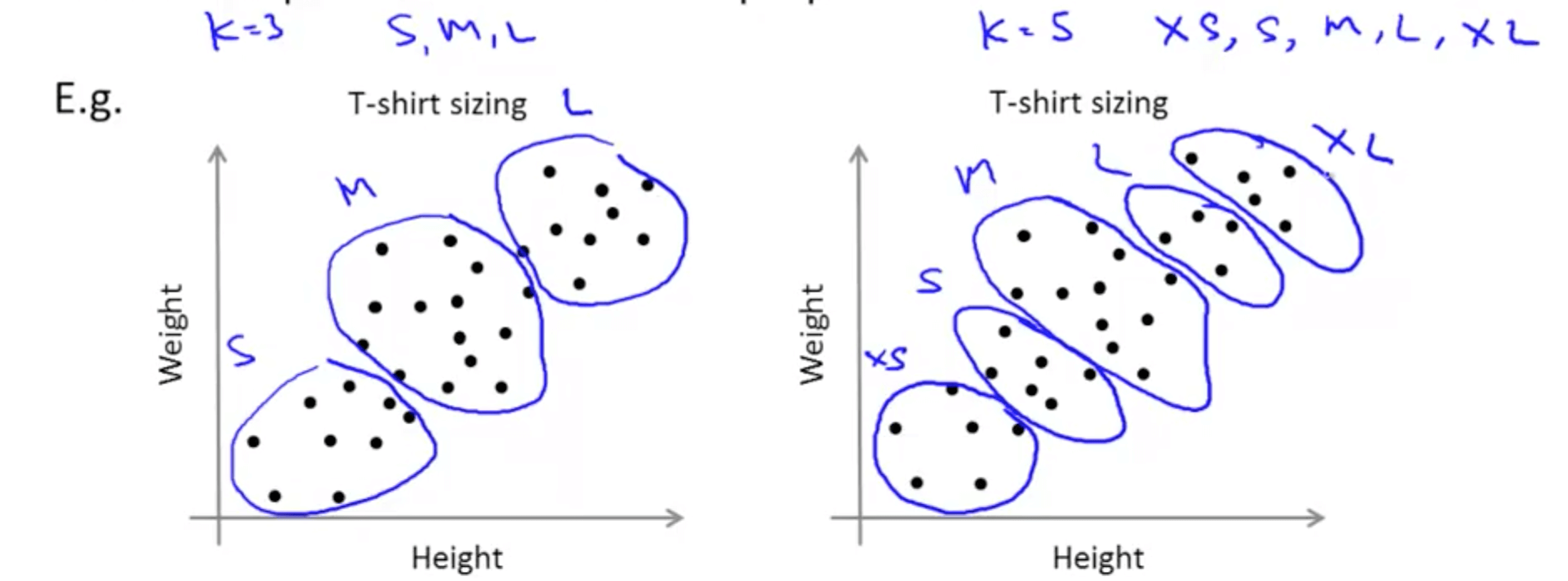
- This would allow us to decide whether we want 3 or 5 clusters
- Elbow method