Game theory is increasingly relevant in reinforcement learning where we have multiple agents. Understand the concept of Nash Equilibrium.
Game Theory¶
- Mathematics of conflict.
- Multiple agents.
- Used in economics.
- Increasingly a part of AI/ML.
1. Two-player zero-sum finite deterministic game of perfect information
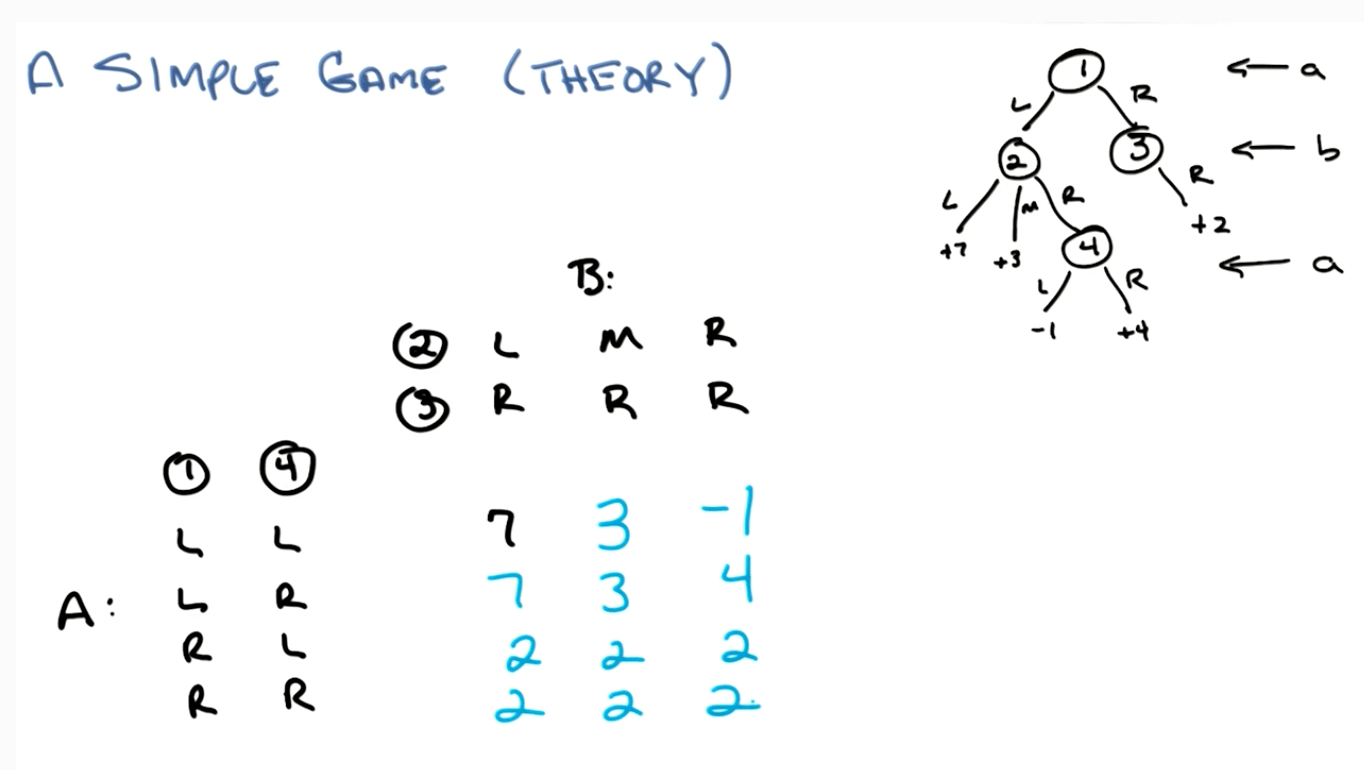
- A's points: leaves.
- B's points: negative of A.
- Pure strategy: 2
- A: maximize
- B: minimize
- Pure strategy: 2
Minimax $\equiv$ Maximax Strategy
- Both A and B would consider the worst case counter strategy.
- A: maximize points.
- B: minimize points.
- There would always have an optimal pure strategy for each player.
- You are assuming they are doing the same thing.
- You are also assuming they are assuming everyone else are doing the same thing.
2. Two-player zero-sum finite non-deterministic game of perfect information
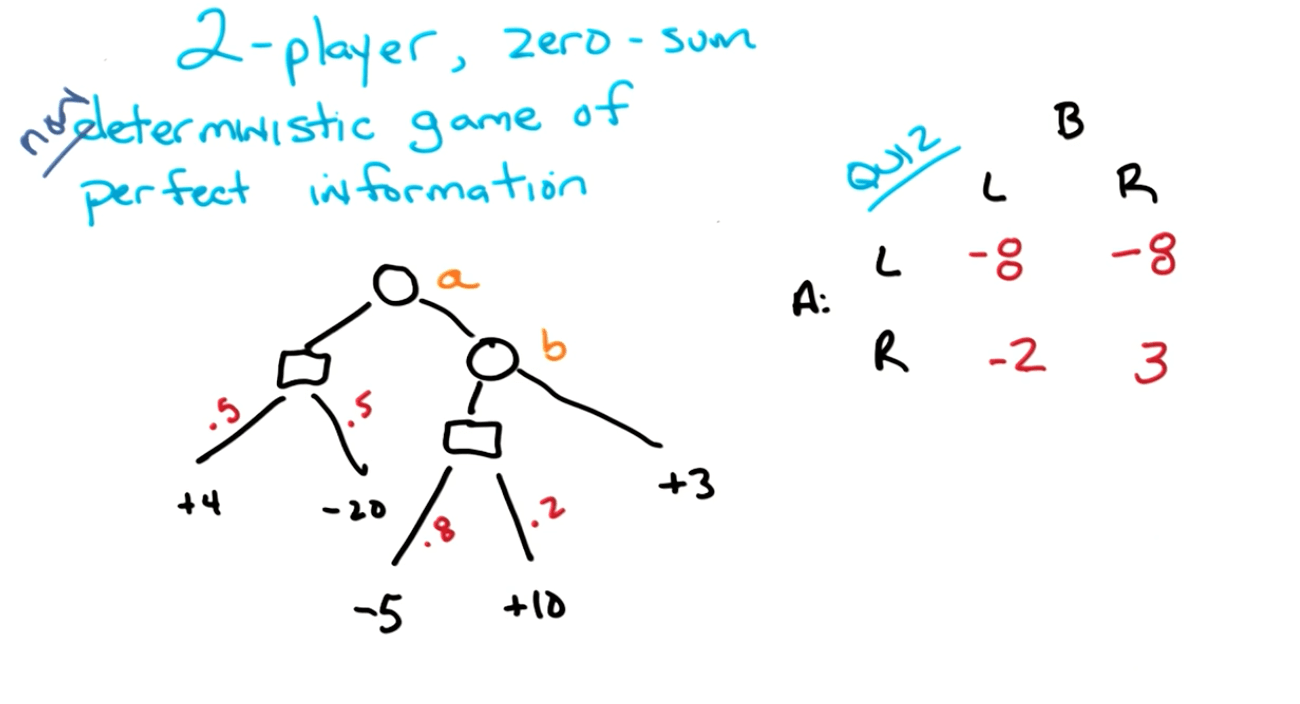
- Pure Strategy: -2
- A would maximize
- B would minimize
- Pure Strategy: -2
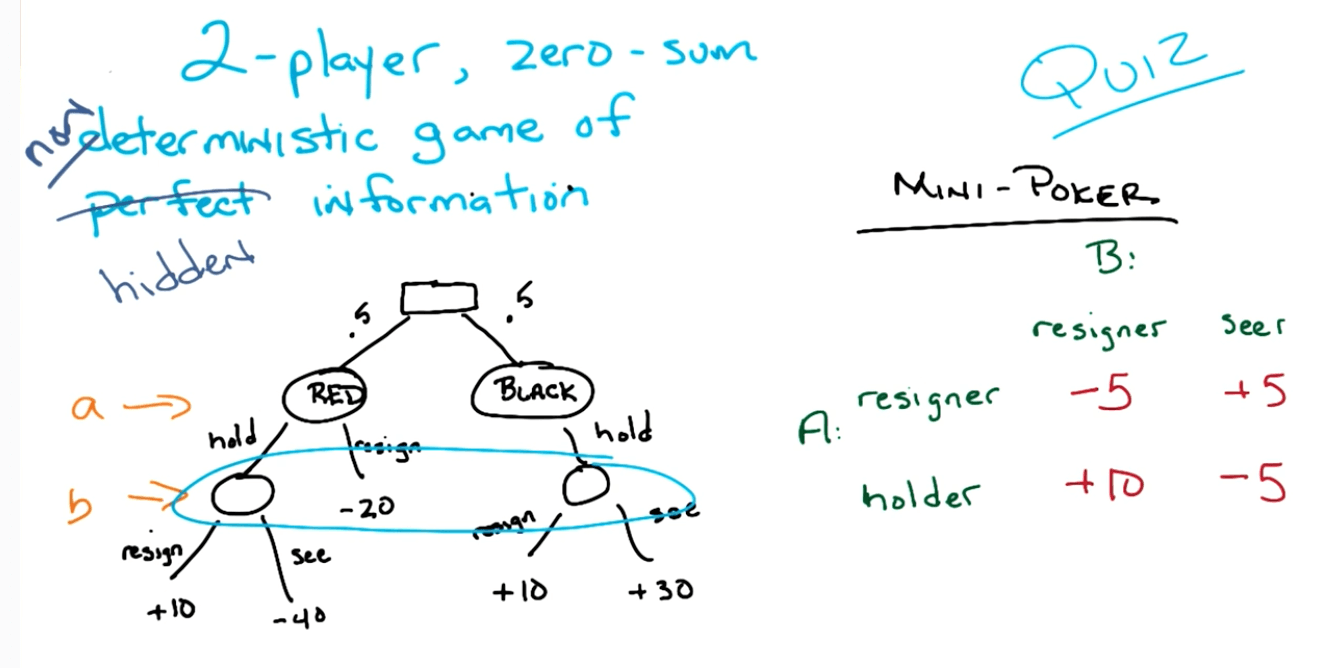
3. Two-player zero-sum finite non-deterministic game of hidden information
- Mini-poker
- A is dealt a card, red or black with a probability of 50% each
- Red is bad for A
- Black is good for A
- A may resign if given a red card: - 20 for A
- Else A can hold:
- B resigns: + 10
- B sees:
- If red: - 40
- If black: + 30
- Else A can hold:
- A is dealt a card, red or black with a probability of 50% each
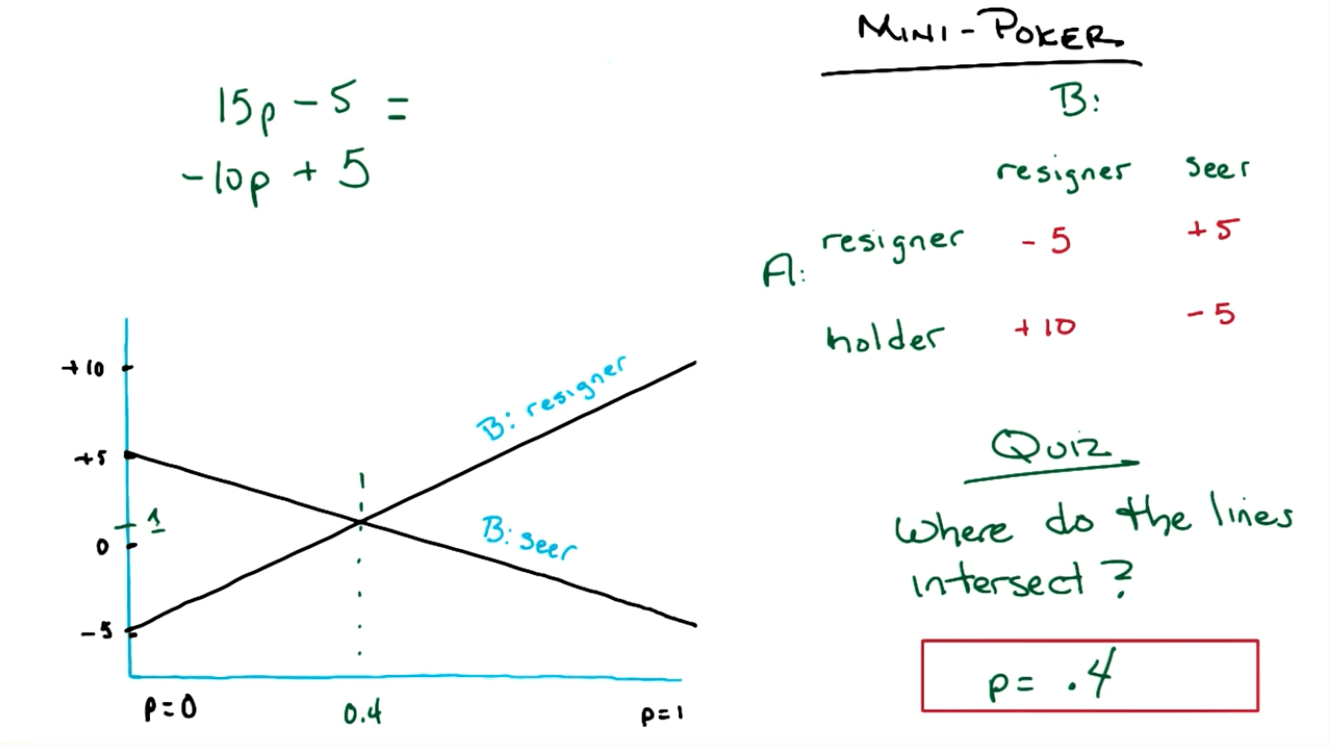
- Minimax is not equal to Maximax in this scenario.
- A's strategy depends on what B would do.
- B's strategy depends on what A would do.
- We can use a mixed strategy here.
- There's a distribution over strategies.
- Assume p is the probability of being a "holder" and A has a mixed strategy.
- B: resigner
- A's expected profit:
- 10p + (1-p)(-5) = 15p - 5
- A's expected profit:
- B: seer
- A's expected profit:
- -5p + (1-p)(5) = -10p + 5
- A's expected profit:
- We equate the equations to find out that we have p=0.4, where the expected value of game is +1.
- B: resigner
4. Two-player non-zero-sum finite non-deterministic game of hidden information
- Typical scenario where the district attorney offers a deal to both criminals to turn on one another.
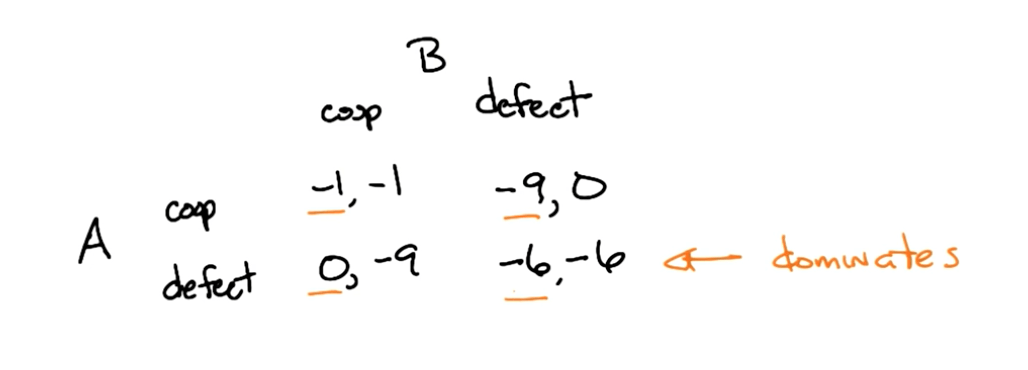
- No matter the response of the other prisoner, both would choose to defect. There is a dominance of a particularly strategy here.
- This is also known as the Prisoner's Dilemma.
Nash Equilibrium
- n players with strategies $S_1, S_2 ... S_n$
- $S^*_1 \in S_1 ... S^*_n \in S_n$ are in Nash Equilibrium if
- $\forall_i \ \ S^*_i = argmax_{s_i} utility_i(S^*_1 ... S^*_n)$ there is no reason for anyone to change.
Nash Equilibrium Notes
- In the n-player pure strategy game, if elimination of strictly dominated strategies elimates all but one combination, that combination is the unique NE.
- Any NE will survive elimination of strictly dominated strategies.
- If n is finite and for all strategies which are finite, then there exist at least one NE.
- If you have n-repeated game, you have n-repeated NE.