Linear Regression with Multiple Variables.
1. Multivariate Linear Regression
I would like to give full credits to the respective authors as these are my personal python notebooks taken from deep learning courses from Andrew Ng, Data School and Udemy :) This is a simple python notebook hosted generously through Github Pages that is on my main personal notes repository on https://github.com/ritchieng/ritchieng.github.io. They are meant for my personal review but I have open-source my repository of personal notes as a lot of people found it useful.
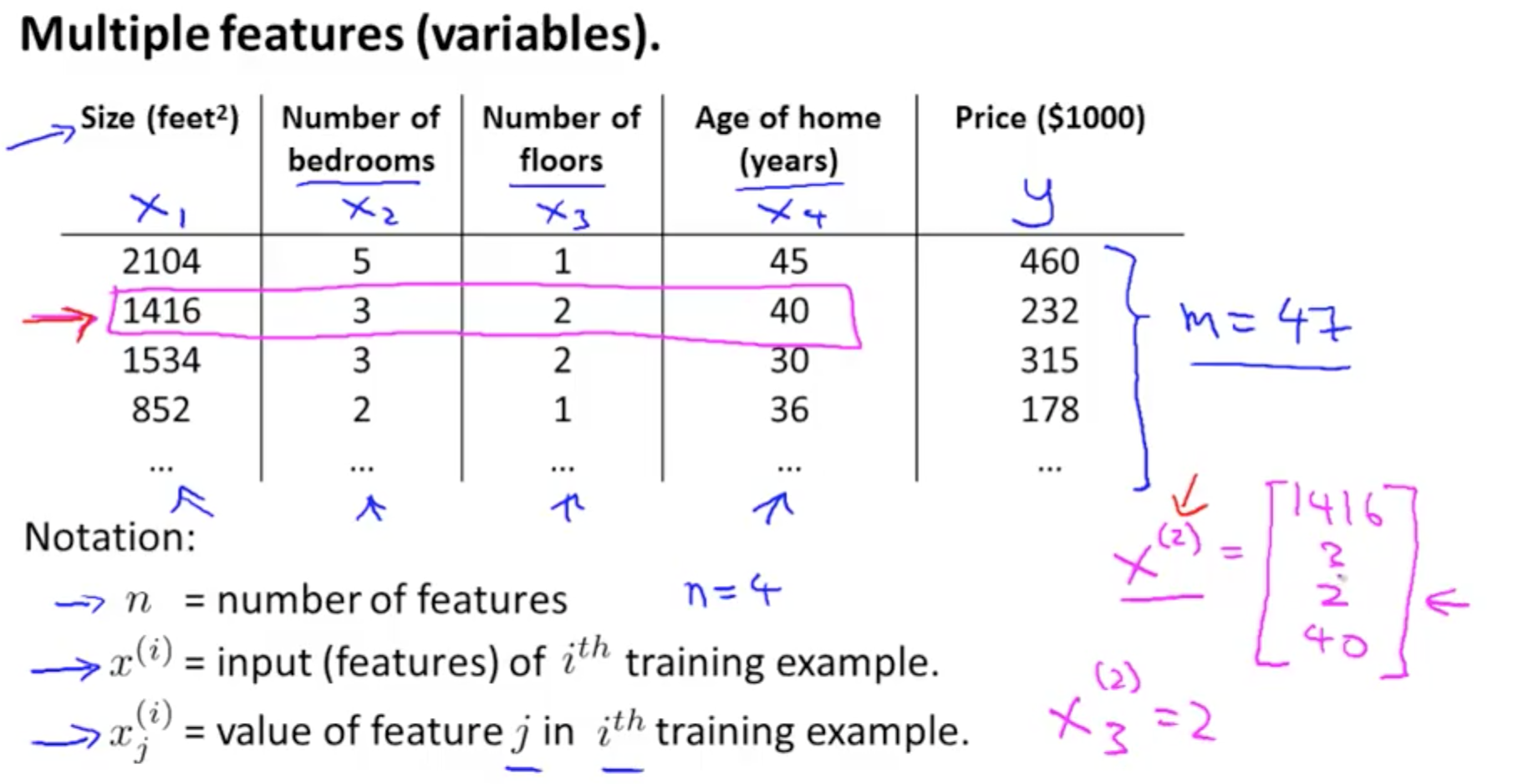
1a. Multiple Features (Variables)
- X1, X2, X3, X4 and more
- New hypothesis
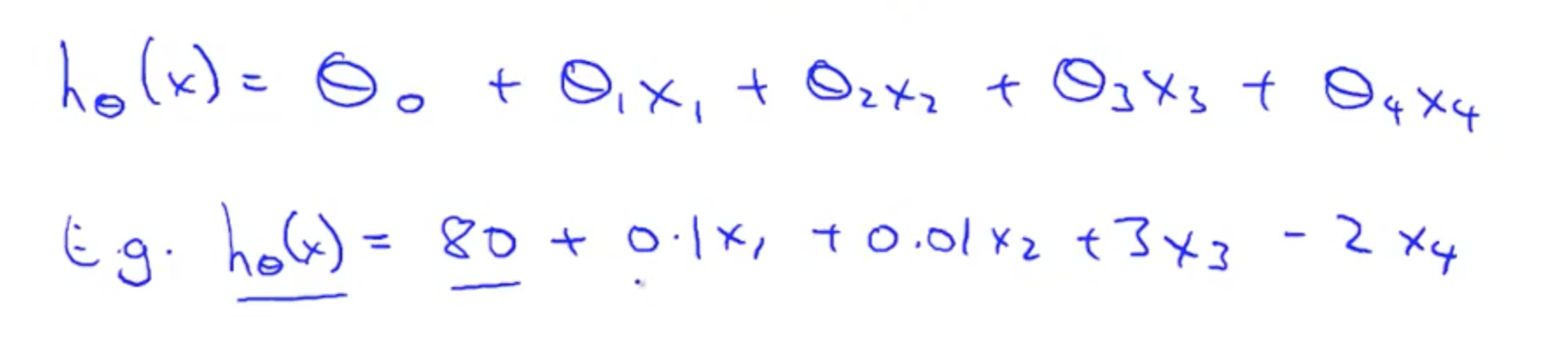
- Multivariate linear regression
- Can reduce hypothesis to single number with a transposed theta matrix multiplied by x matrix
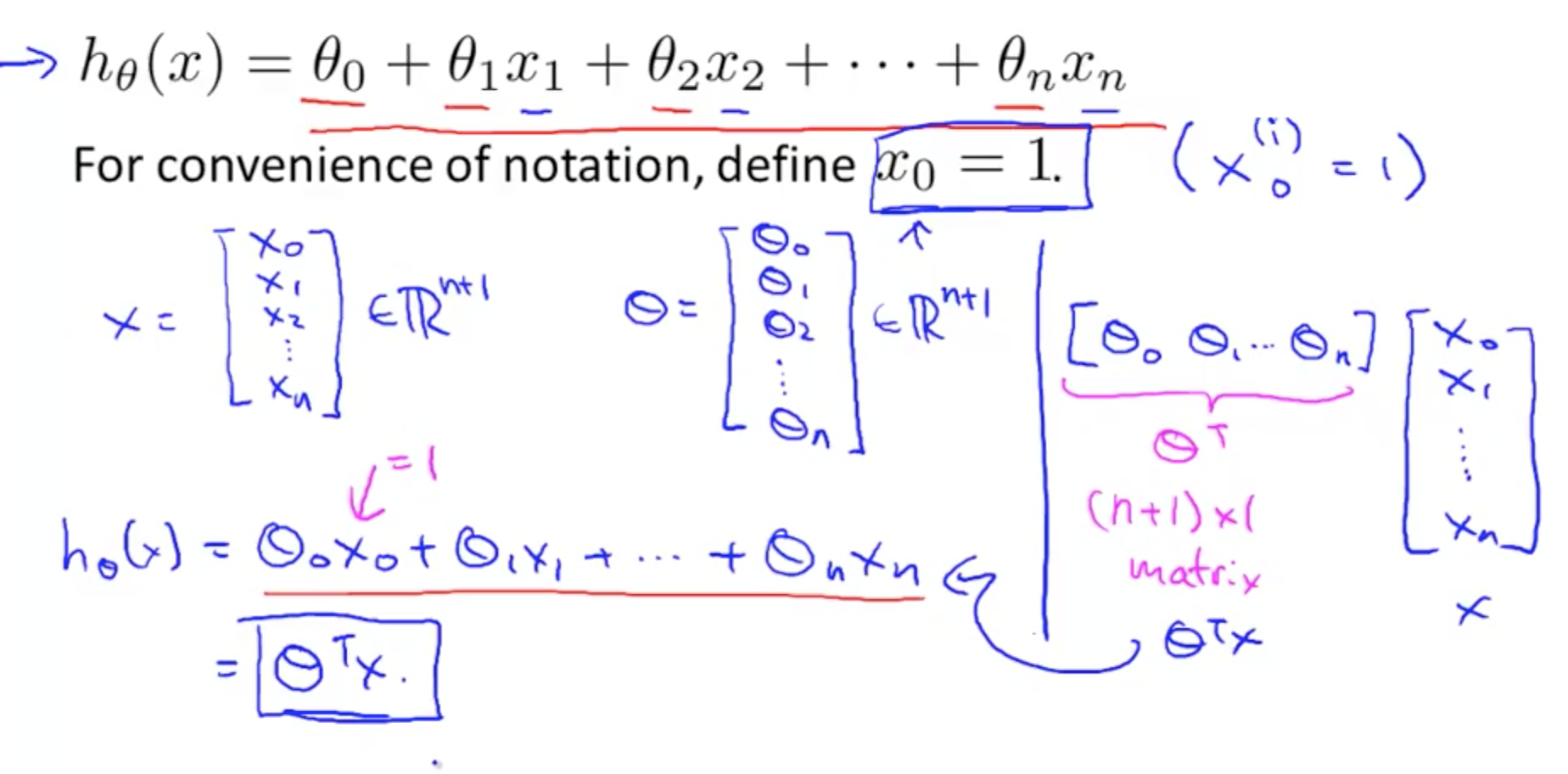
- Can reduce hypothesis to single number with a transposed theta matrix multiplied by x matrix
1b. Gradient Descent for Multiple Variables
- Summary


- New Algorithm

1c. Gradient Descent: Feature Scaling
- Ensure features are on similar scale
- Gradient descent will take longer to reach the global minimum when the features are not on a similar scale
- Feature scaling allows you to reach the global minimum faster
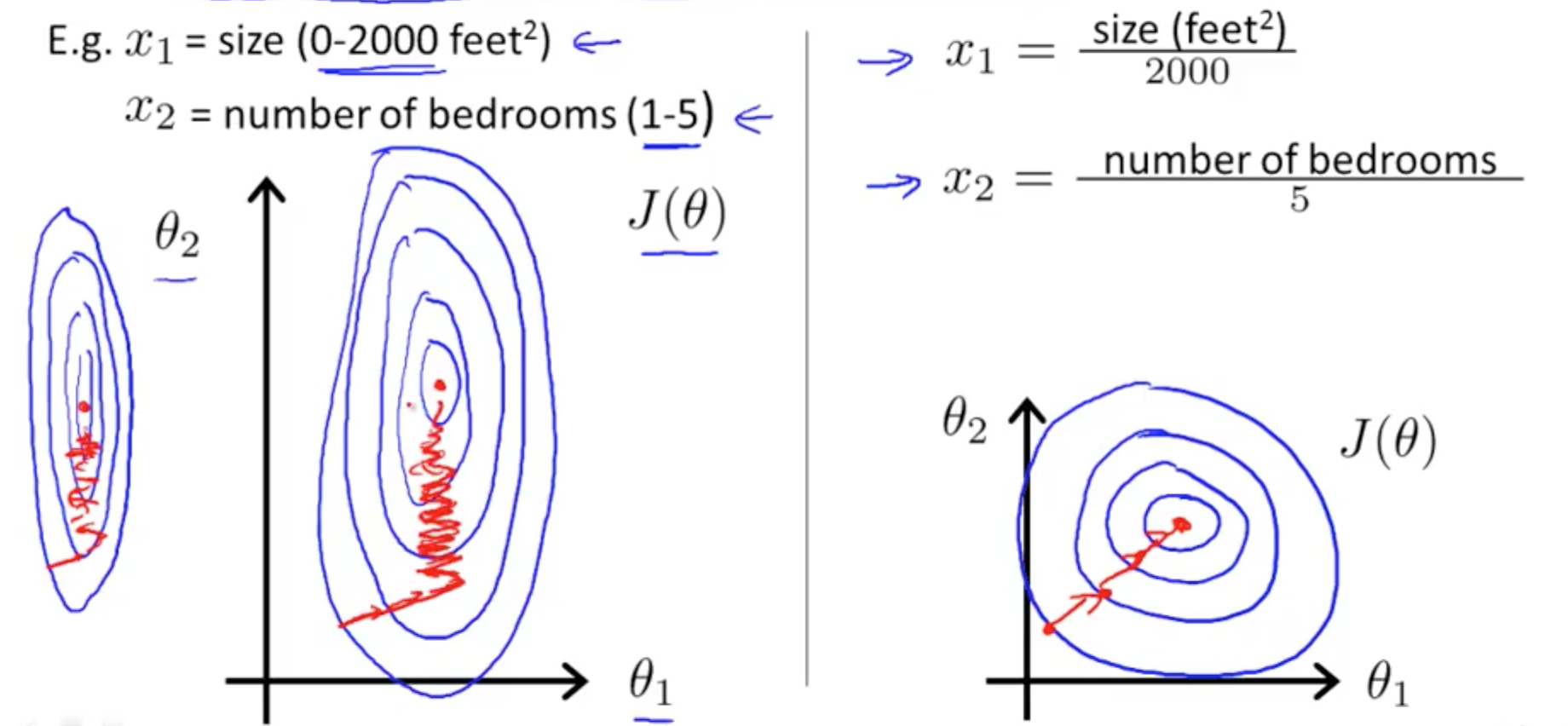
- So long they’re close enough, need not be between 1 and -1

- Mean normalization

1d. Gradient Descent: Checking
- Can you a graph
- x-axis: number of iterations
- y-axis: min J(theta)
- Or use automatic convergence test
- Tough to gauge epsilon

- Tough to gauge epsilon
- Gradient descent that is not working (large learning rate)
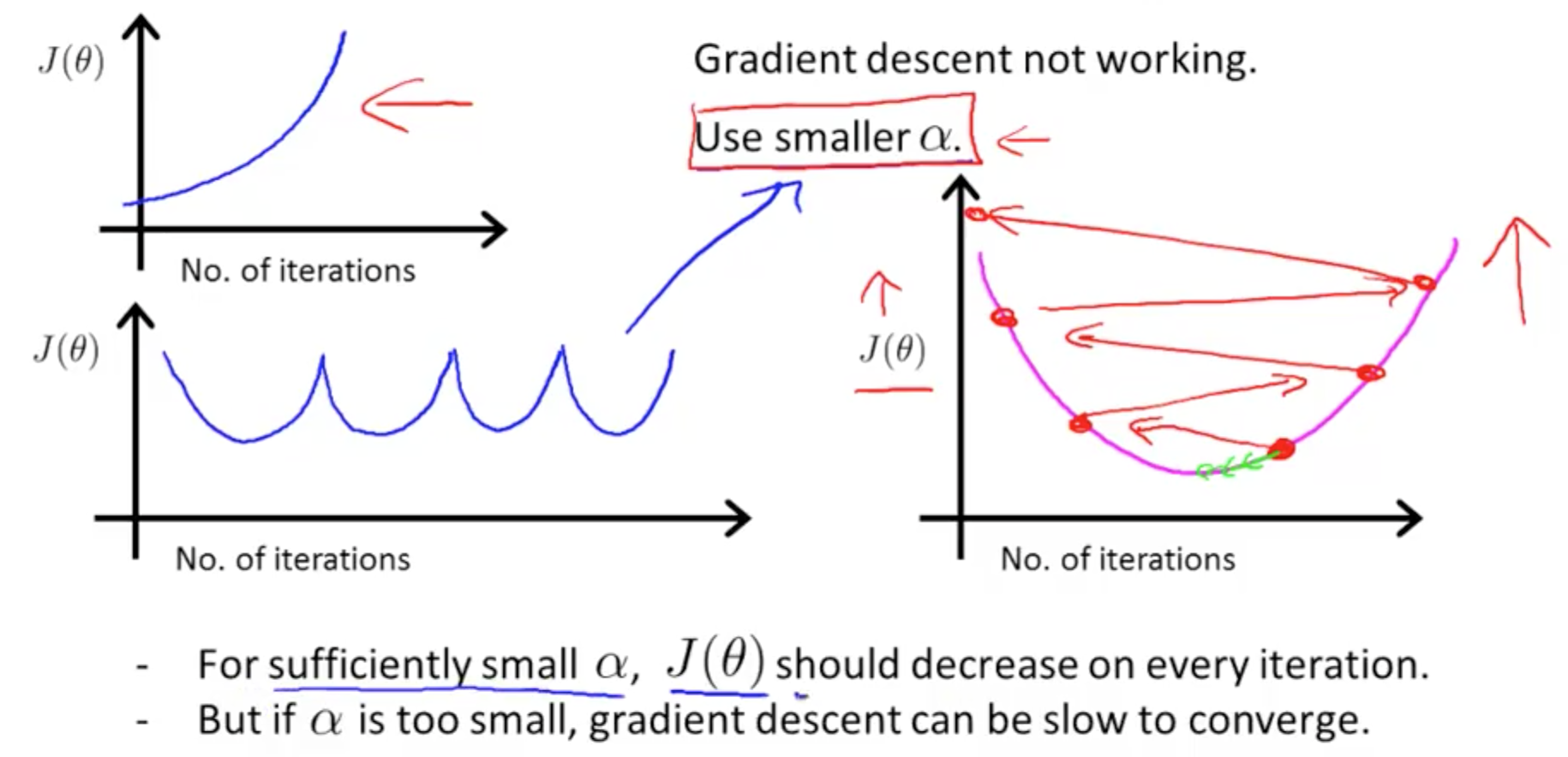
1e. Gradient Descent: Learning Rate
- Alpha (Learning Rate) too small: slow convergence
- Alpha (Learning Rate) too large:
- J(theta) may not decrease on every iteration
- May not converge (diverge)
- Start with 0.001 and increase x3 each time until you reach an acceptable alpha
- Choose a slightly smaller number than that acceptable alpha value
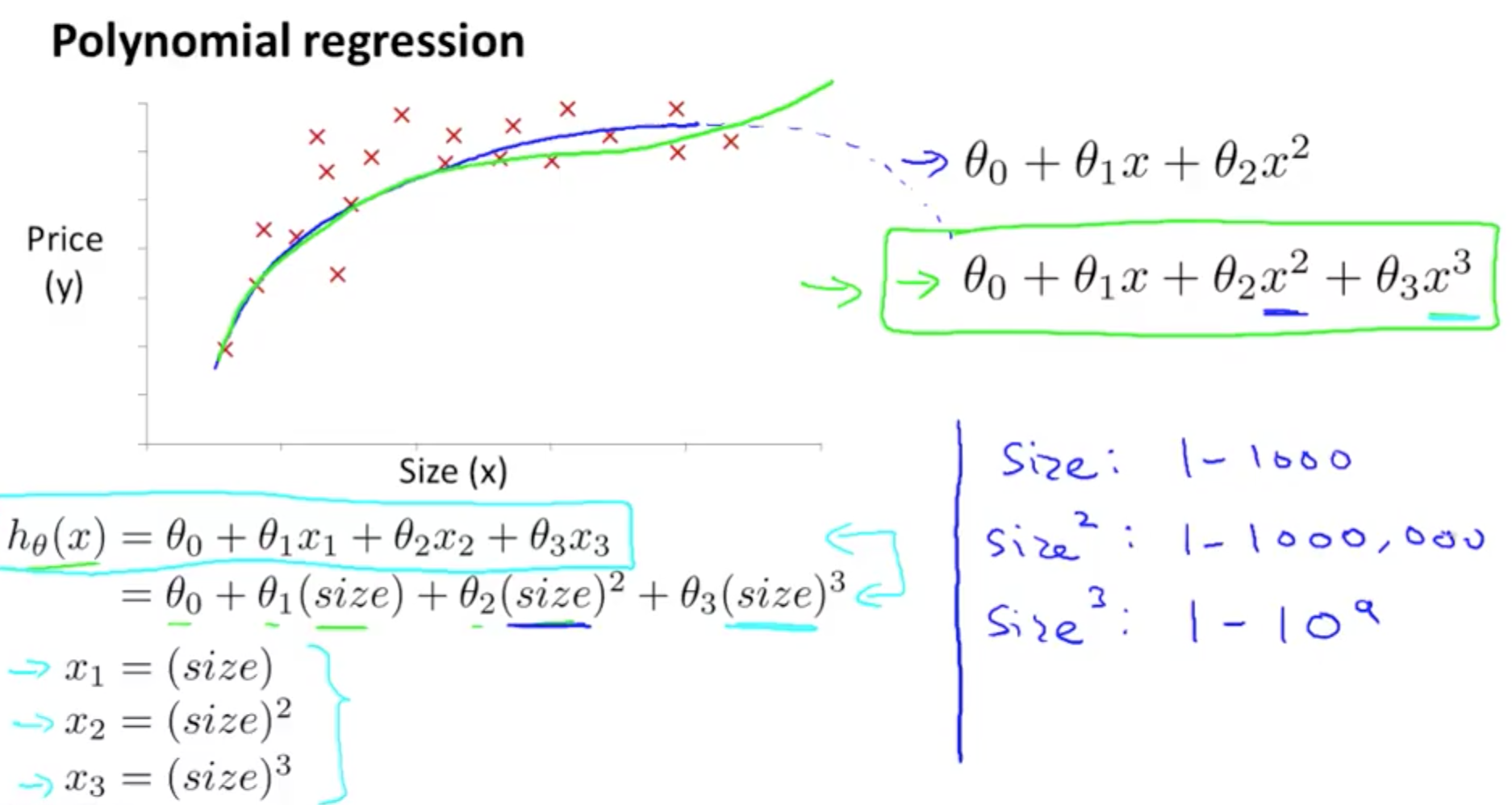
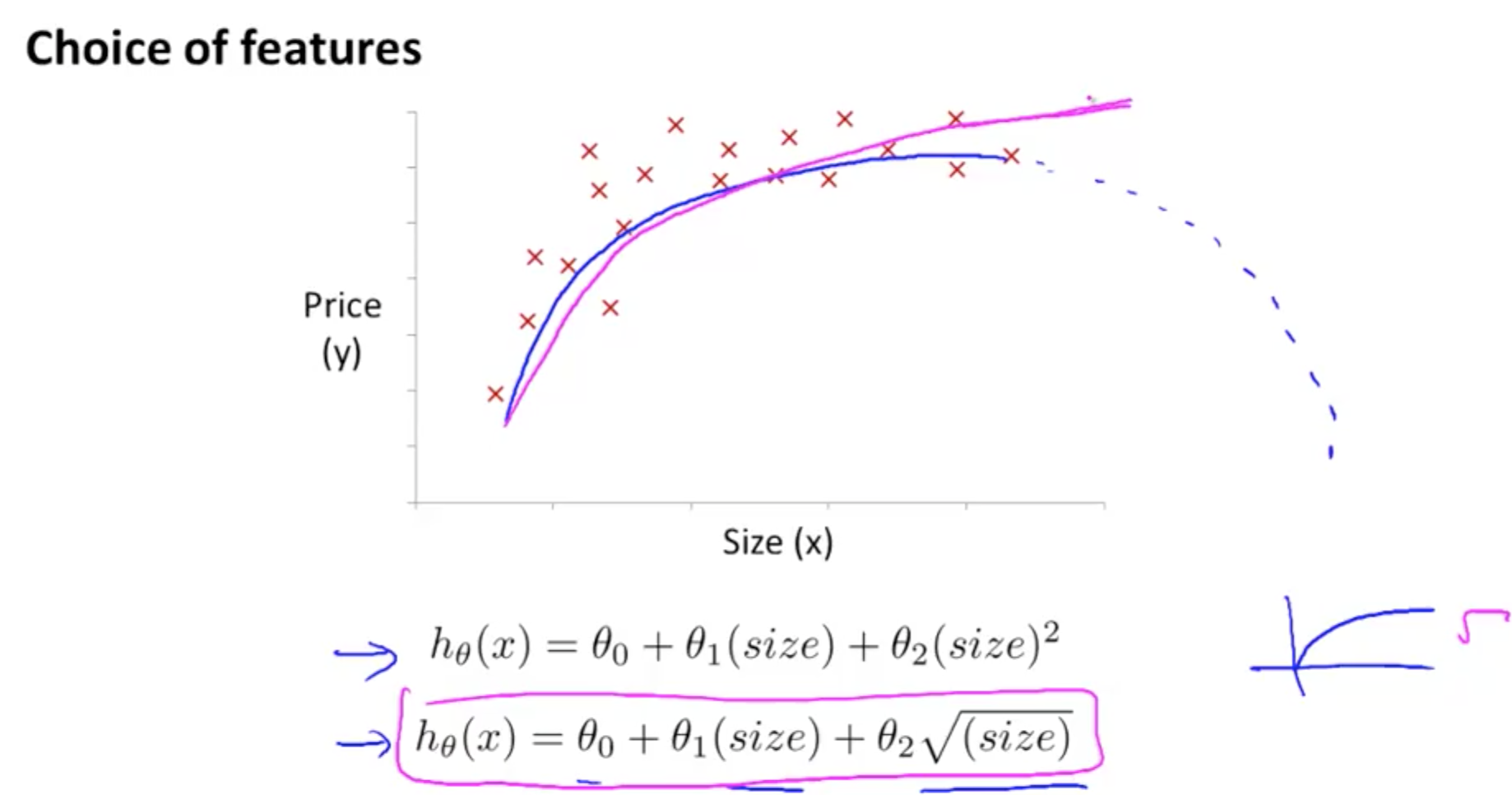
1f. Features and Polynomial Regression
- Ensure the features capture the pattern
- Doesn’t make sense to choose quadratic equation for house prices
- Use cubic or square root
- There are automatic algorithms, and this will be discussed later
2. Computing Parameters Analytically
2a. Normal Equation
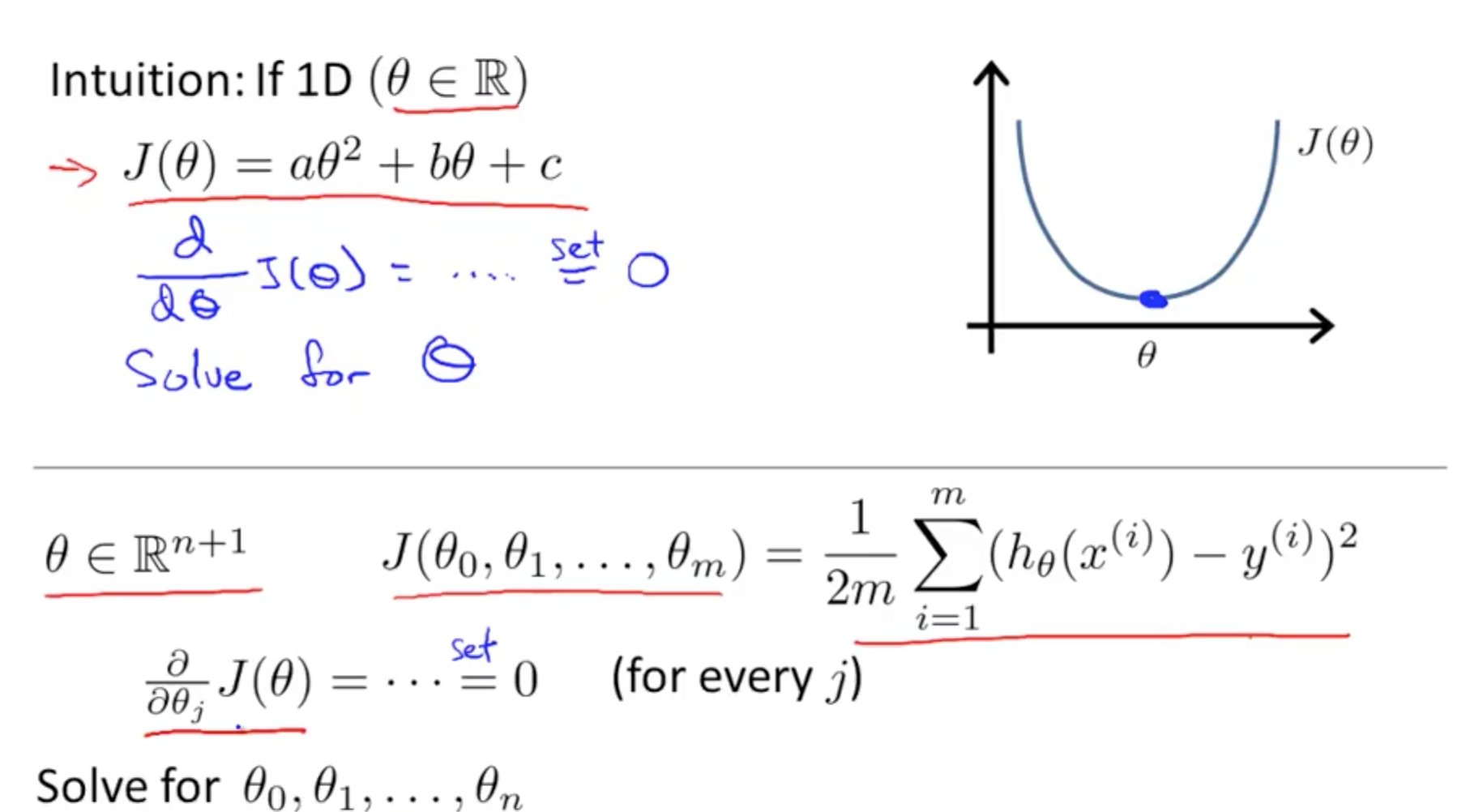
- Method to solve for theta analytically
- If theta is real number
- Minimise J(theta) is to take the derivative and equate to zero
- Solve for theta
- If theta is not
- Take partial derivative and equate to zero
- Solve for all thetas
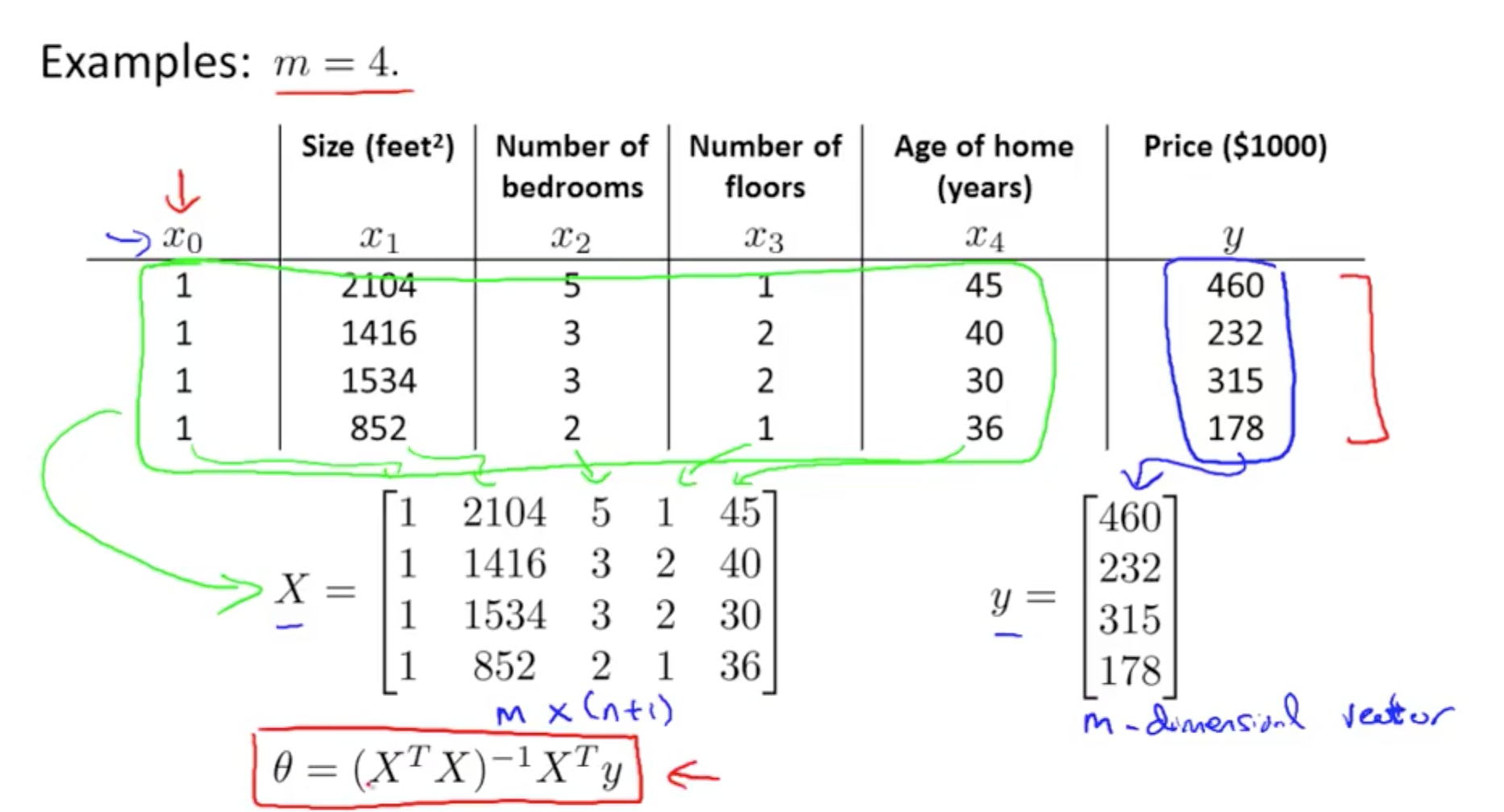
- Minimise Cost Function: Specific Example
- X: m x (n + 1)
- m: number of training examples
- n: number of features
- X_transpose: (n + 1) x m
- X_transpose * X: (n + 1) x m * m x (n + 1) = (n + 1) x (n + 1)
- (X_transpose * X)^-1 * X_transpose: (n + 1) x (n + 1) * (n + 1) x m = (n + 1) x m
- theta = (n + 1) x m * m x 1 = (n + 1) x 1
- X: m x (n + 1)
- Minimise Cost Function: General
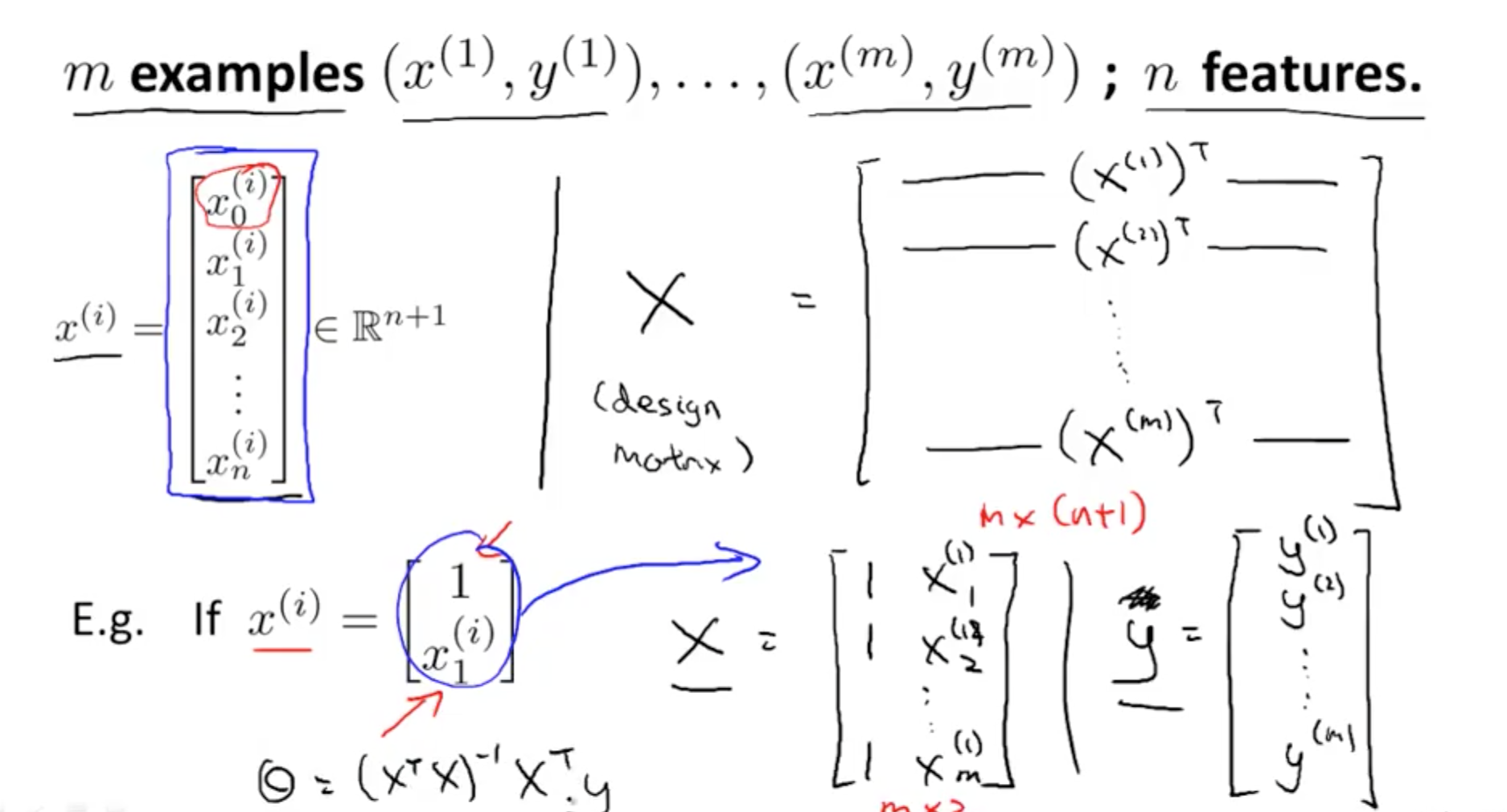
- Minimise Cost: Octave Code
- No need for feature scaling using normal equation
pinv (X' * X) * X' * y
- Gradient Descent vs Normal Equation
| Gradient Descent | Normal Equation |
|---|---|
| Need to choose alpha | No need to choose alpha |
| Needs many iterations | Don’t need to iterate |
| Works with large n (10,000) | Slow if n is large (100, 1000 is fine) |
| Number of features > 1000 | So long number features < 1000 |
2b. Normal Equation Non-invertibility
- What happens if X_transpose * X is non-invertible (singular or degenerate)
pinv (X' * X) * X' * y- This works regardless if it is non-invertible
- Intuition of non-invertibility
- Causes of non-invertibility

- Delete redundant features to solve non-invertibility problem
- Delete some features or use regularization
- Causes of non-invertibility