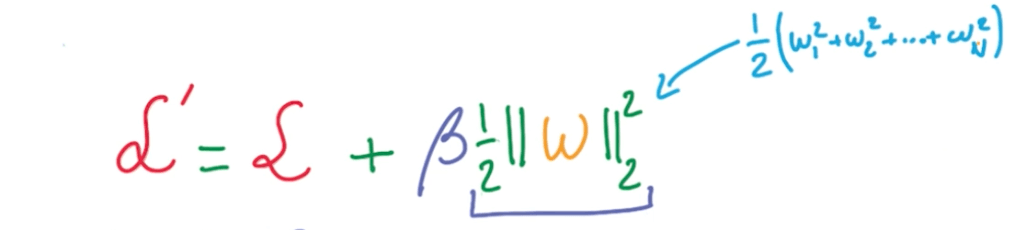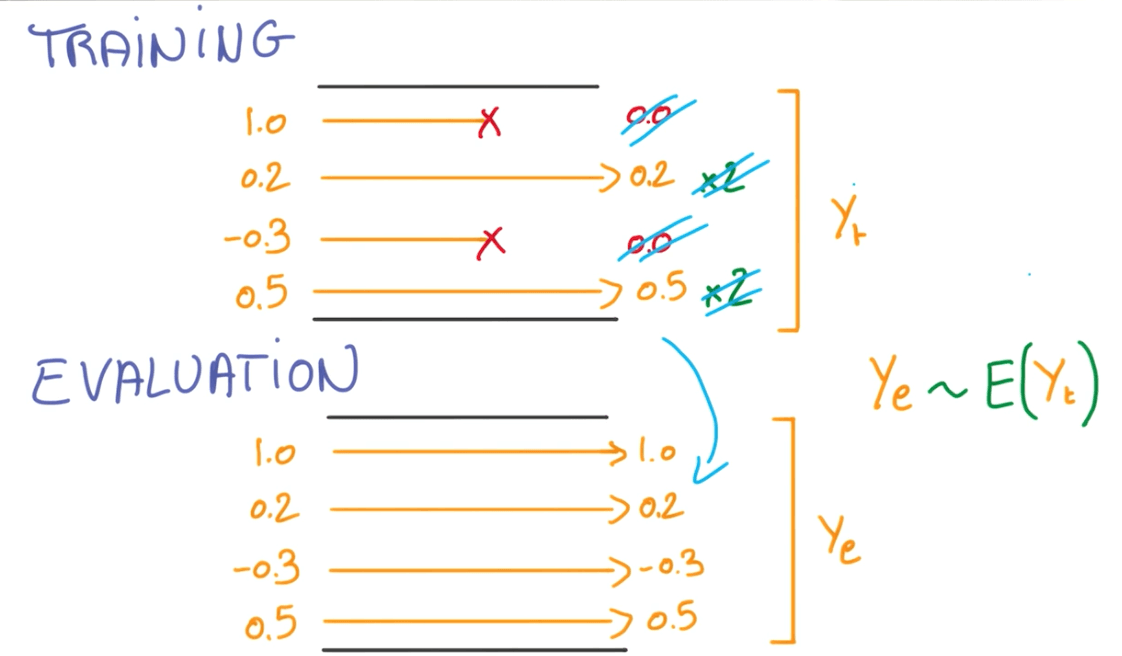Build a deep neural network with ReLUs and Softmax.

Deep Neural Networks: Introduction¶

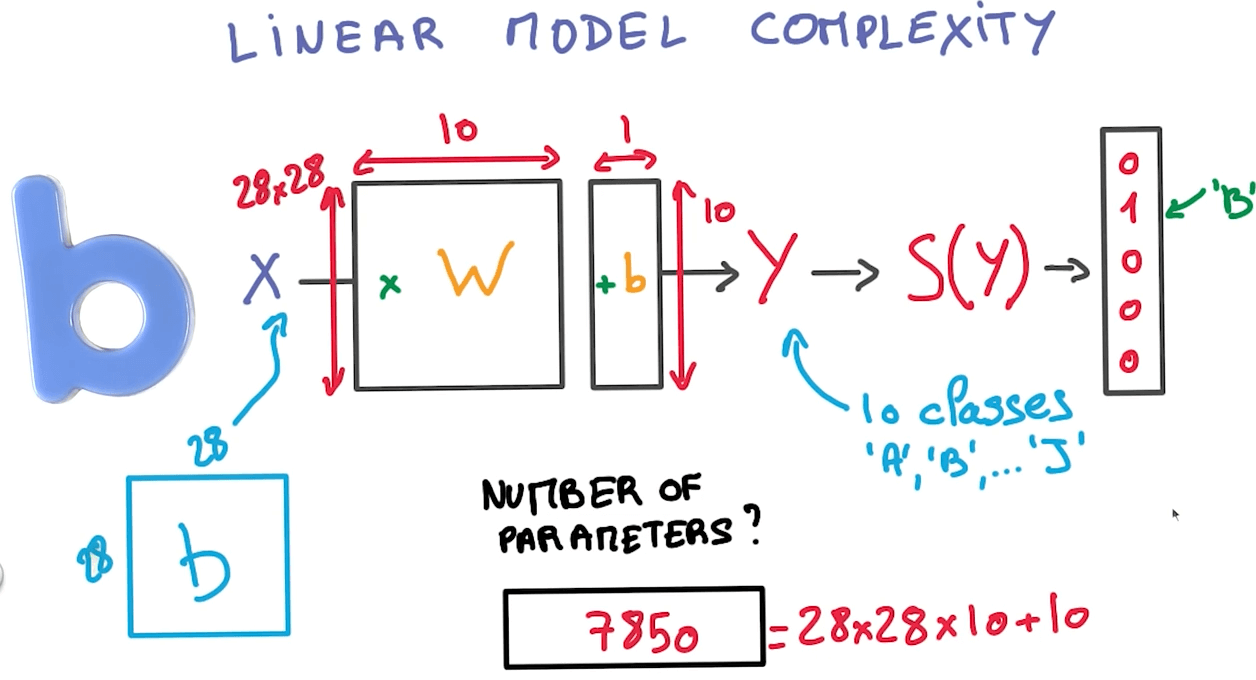
Linear Model Complexity

• If we have N inputs and K outputs, we would have:
  • (N+1)K parameters
  • 
• Limitation
  • $y = x_1 + x_2$ can be represented well
  • $y = x_1 * x_2$ cannot be represented well
• Benefits
  • Derivatives are constants

Rectified Linear Units (ReLUs)

• This is a non-linear function.
• 
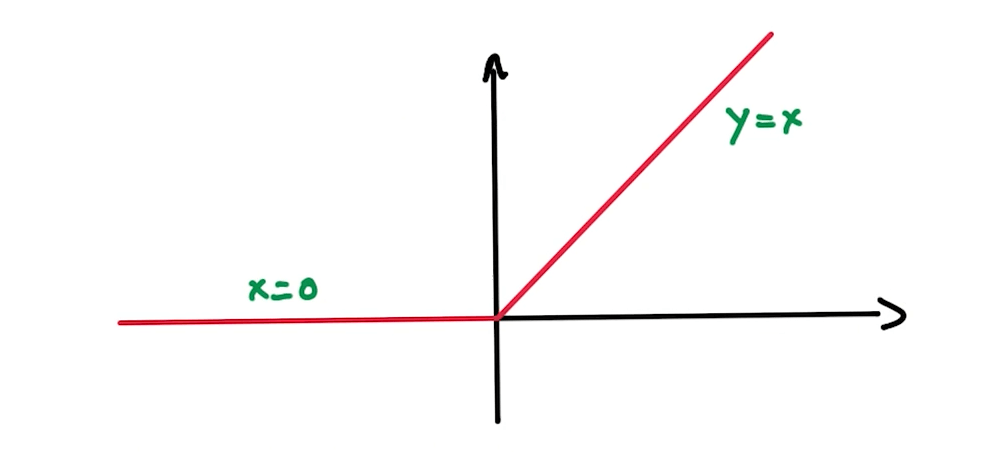
  • Derivatives are nicely represented too.
    • 

Network of ReLUs: Neural Network

• We can do a logistic classifier and insert a ReLU to make a non-linear model.
  • 
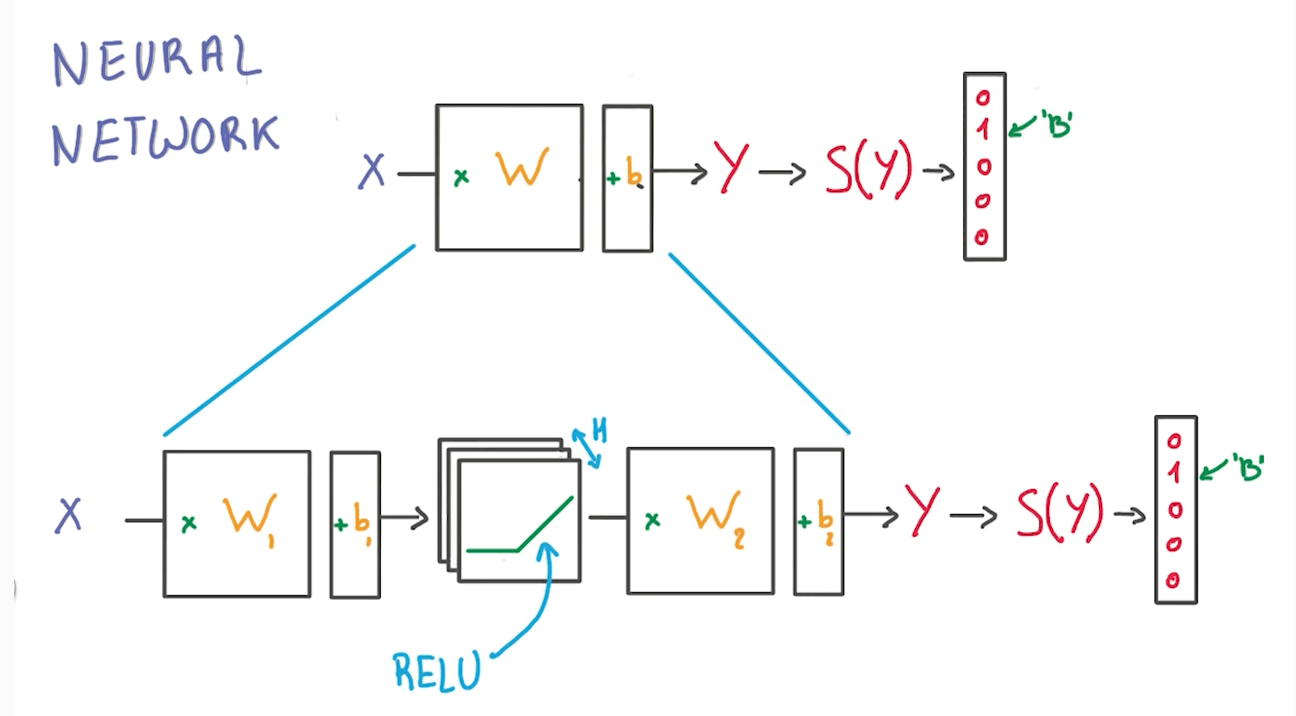
  • H: number of RELU units

2-Layer Neural Network

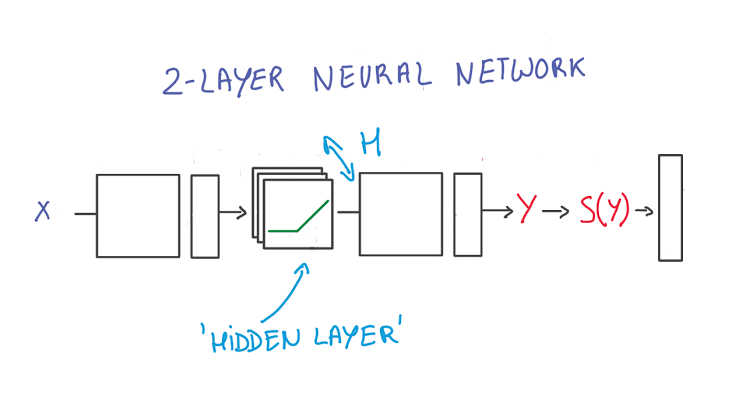
1. The first layer effectively consists of the set of weights and biases applied to X and passed through ReLUs. The output of this layer is fed to the next one, but is not observable outside the network, hence it is known as a hidden layer.
2. The second layer consists of the weights and biases applied to these intermediate outputs, followed by the softmax function to generate probabilities.
   • A softmax regression has two steps: first we add up the evidence of our input being in certain classes, and then we convert that evidence into probabilities.

Stacking Simple Operations

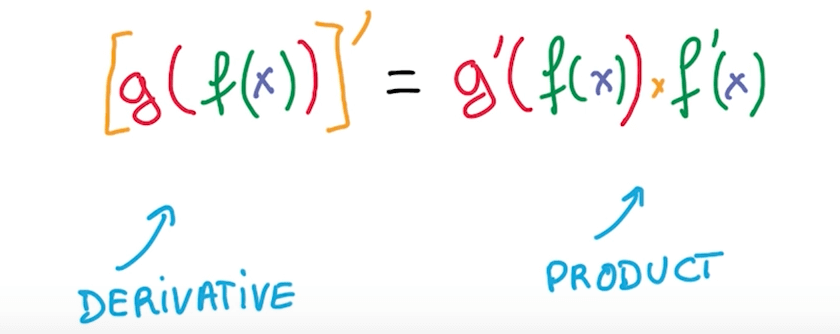
• We can compute derivative of function by taking product of derivatives of components.

Backpropagation

• Forward-propagation
  • You will have data X flowing through your NN to produce Y.
• Back-propagation
  • Your labelled data Y flows backward to calculate "errors" of our calculations.
  • You will be calculating the gradients ("errors"), multiply it by a learning rate, and use it to update our weights.
  • We will be doing this many times.

Go Deeper

• It is better go deeper than increasing the size of the hidden layers (by adding more nodes)
  • It gets hard to train.
• We should go deeper by adding more hidden layers.
  • You would reap parameter efficiencies.
  • However you need large datasets.
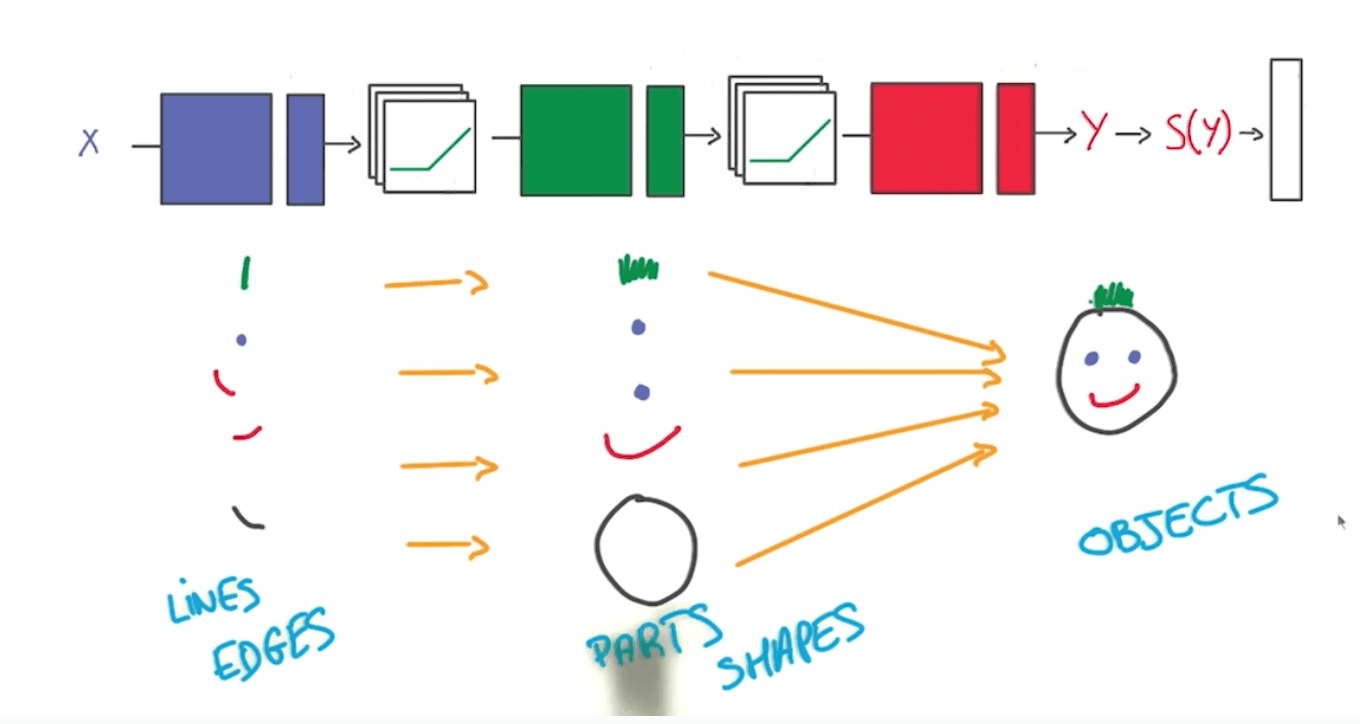
  • Also, deep models can capture certain structures well such as the following.
    • 

Regularization

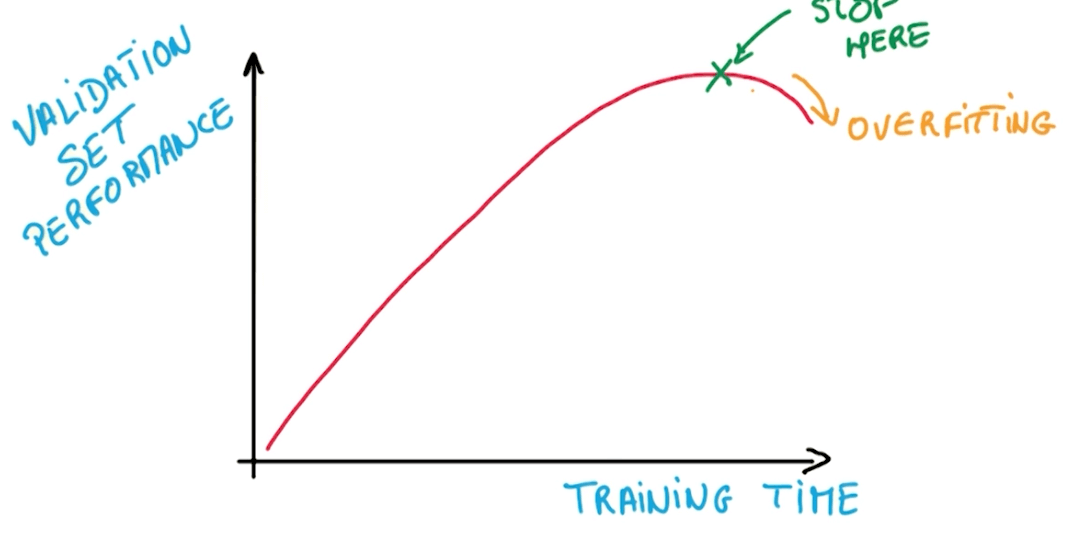
• We normally train networks that are bigger than our data.
  • Then we try to prevent overfitting with 2 methods.
    • Early termination
      • 
    • Regularization
      • Applying artificial constraints.
      • Implicitly reduce number of free parameters while enabling us to optimize.
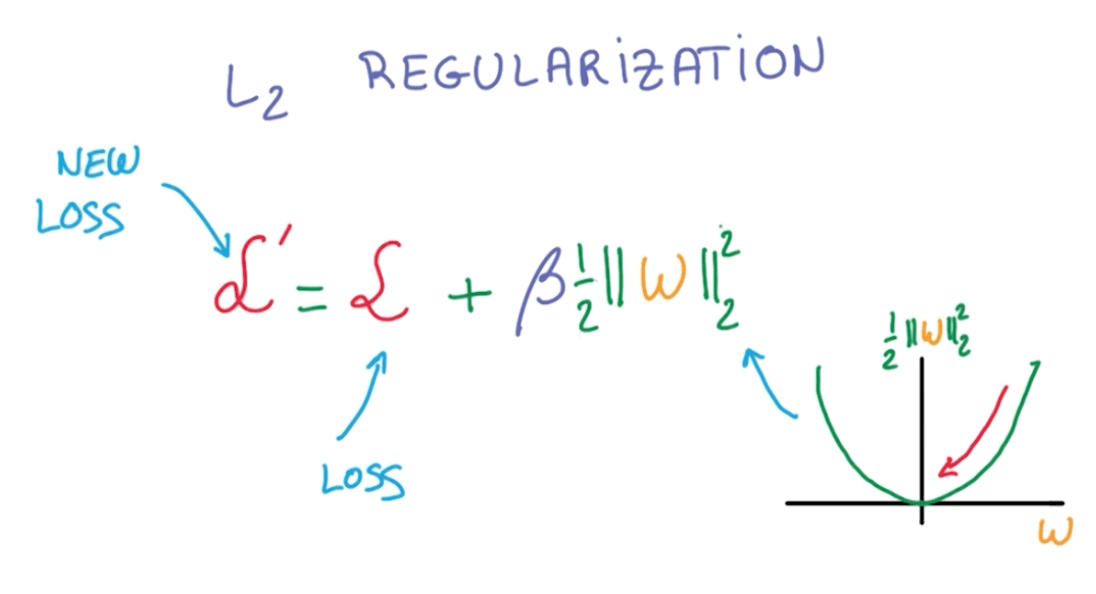
      • L2 Regularization
        • We add another term to the loss that penalizes large weights.
        • This is simple because we just add to our loss.
        • 

L2 Regularization's Derivative

• The norm of w is the sum of squares of the elements in the vector.
  • The equation:
    • 
  • The derivative:
    • $ (\frac {1}{2} w^2)' = w $

L2 Regularizatin: Dropout

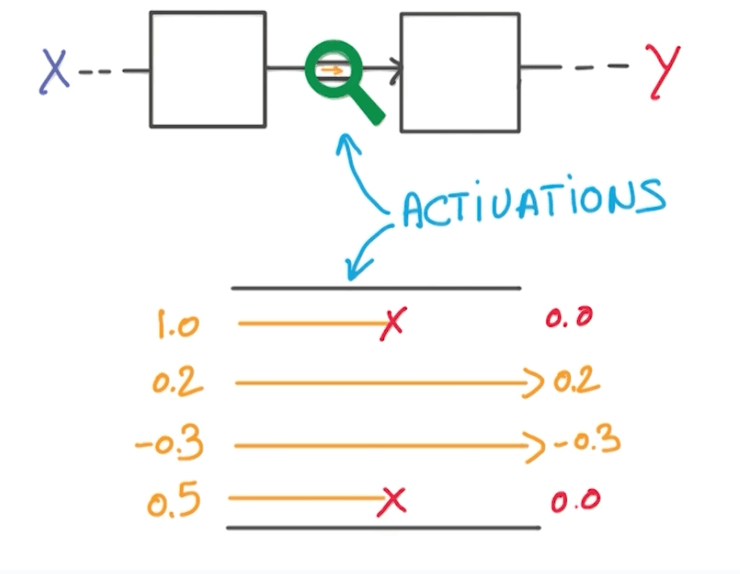
• Your input goes through an activation function.
  • During the activation function, we randomly take half of the data and set to 0.
  • We do this multiple times.
    • 
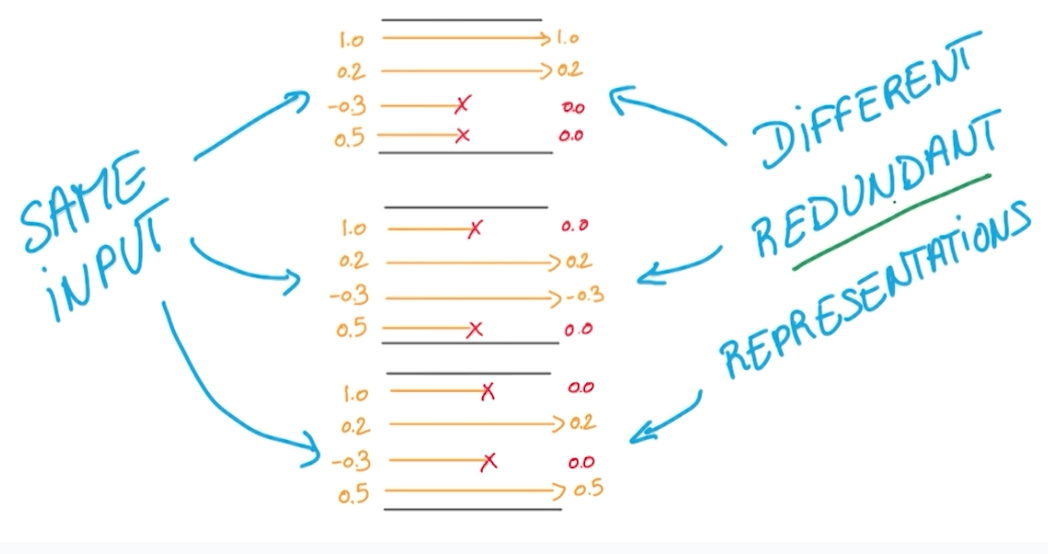
• We are forced to learn redundant information.
  • It's like a game of whack-a-mole.
  • There's always one or more that represents the same thing.
    • 
• Benefits
  • It prevents overfitting.
  • It makes network act like it's taking a consensus of an ensemble of networks.

Dropout during Evaluation

• We would take the expectation of our training y's.
  • 

Tags: machine_learning